Магнитная энергия атомов

Теперь я снова хочу поговорить о магнитном моменте. Я уже говорил, что в квантовой механике магнитный момент атомной системы может быть связан с моментом количества движения соотношением (34.6):

где - q_e— заряд, а m — масса электрона.

Атомные магнитики, будучи помещены во внешнее магнит­ное поле, приобретут дополнительную магнитную энергию, которая зависит от компоненты их магнитного момента в на­правлении поля. Мы знаем, что

U_маг =-m•В. (34.28) Выбирая ось z вдоль направления поля В, получаем

U _маг =m_zВ. (34.29) А используя уравнение (34.27), находим

Согласно квантовой механике, величина J_z может принимать только такие значения: jh, (j-1)h,...,- jh. Поэтому магнитная энергия атомной системы не произвольна, допустимы только некоторые ее значения. Например, максимальная величина энергии равна

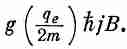
Величину q_eh/2m обычно называют «магнетоном Бора» и обоз­начают через m _B:

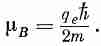
Возможные значения магнитной энергии будут следующими:

где J_z/h принимает одно из следующих значений: j, (j-1), (j-2),..., (-j+1), -j.

Другими словами, энергия атомной системы, помещенной в магнитное поле, изменяется на величину, пропорциональную полю и компоненте J_г. Мы говорим, что энергия атомной маг­нитной системы «расщепляется магнитным полем на 2j+1 уровня». Например, атомы со спином j=³/₂, энергия которых вне магнитного поля равна U₀, в магнитном поле будут иметь четыре возможных значения энергии. Эти энергии можно изобра­зить на диаграмме энергетических уровней наподобие фиг. 34.5.

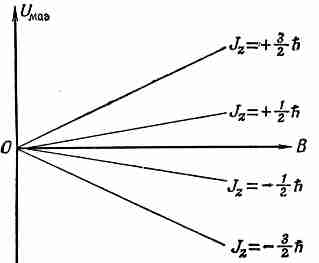
Фиг. 34.5. Возможные магнит­ные энергии атомной системы со спином ³/₂ в магнитном поле В.

Однако энергия каждого атома в данном поле В принимает только одно из четырех возможных значений. Именно это гово­рит квантовая механика о поведении атомной системы в маг­нитном поле.

Простейшая «атомная» система — отдельный электрон. Спин электрона равен ^J/₂, поэтому у него возможны два состояния: J_z=h/2 и J_z=-h /2. Для спинового магнитного момента от­дельного покоящегося электрона (у которого отсутствует орбитальное движение) g=2, так что магнитная энергия будет ±m_BB. На фиг. 34.6 показаны возможные энергии электрона в магнитном поле.

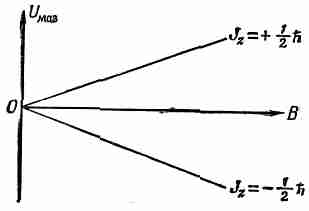
Фиг. 34.6. Два возможных энергетических состояния электрона в магнитном поле В.

Грубо говоря, спин электрона направлен либо «вверх» (по магнитному полю), либо «вниз» (против поля).

У системы с более высоким спином число состояний тоже больше. Поэтому мы можем в зависимости от величины J_z говорить о спине, направленном «вверх» или «вниз» или под некоторым «углом».

Эти результаты квантовой механики мы будем использо­вать при обсуждении магнитных свойств материалов в следую­щей главе.

Дата добавления: 2015-08-20