Диамагнетизм

Рассмотрим теперь с классической точки зрения диамагнетизм. К этому можно подойти несколькими путями, но один из лучших такой. Предположим, что по соседству с атомом мед­ленно включается магнитное поле. При изменении магнитного поля благодаря магнитной индукции будет генерироваться электрическое поле. По закону Фарадея контурный интеграл от Е по замкнутому контуру равен скорости изменения магнит­ного потока через этот контур. Предположим, что в качестве контура Г мы выбрали окружность радиусом r, центр которой совпадает с центром атома (фиг. 34.4).

Фиг. 34.4. Индуцированные элект­рические силы, действующие на элект­роны в атоме.

Среднее тангенциальное электрическое поле Е на этом контуре определяется выраже­нием

т. е. возникает циркулирующее электрическое поле, напряжен­ность которого равна

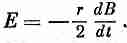
Индуцированное электрическое поле, действуя на атомный электрон, создает момент силы, равный -q_eEr, который дол­жен быть равен скорости изменения момента количества дви­жения dJ/dt:

Интегрируя теперь по времени, начиная с нулевого поля, мы находим, что изменение момента количества движения из-за включения поля будет равно

Это и есть тот дополнительный момент количества движения, который сообщается электрону за время включения поля.

Такой добавочный момент количества движения приводит к добавочному магнитному моменту, который благодаря тому, что это орбитальное движение, равен просто произведению - q_e/2m на момент количества движения. Наведенный диамаг­нитный момент

Знак минус (как можно убедиться непосредственно из закона Ленца) означает, что направление добавочного момента проти­воположно магнитному полю.

Мне бы хотелось написать выражение (34.16) несколько по-иному. Появившаяся у нас величина r² представляет собой рас­стояние от оси, проходящей через атом и параллельной полю В, так что если поле В направлено по оси z, то оно равно x²+y². Если мы рассмотрим сферически симметричные атомы (или усредним по атомам, естественные оси которых могут распола­гаться во всех направлениях), то среднее от z²+y² равно ²/₃ среднего квадрата истинного радиального расстояния от центра атома. Поэтому уравнение (34.16) обычно более удобно записы­вать в виде

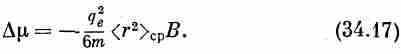
Во всяком случае, мы нашли, что индуцированный атомный момент пропорционален магнитному полю В и противоположен ему по направлению. Это и есть диамагнетизм вещества. Именно этот магнитный эффект ответствен за малые силы, действующие на кусочек висмута в неоднородном магнитном поле.(Вы можете определить величину этой силы, воспользовавшись выражением для энергии наведенного момента в поле и результатами изме­рений изменения энергии при движении образца в область сильного поля или из нее.)

Но перед нами все еще стоит такая проблема: чему равен средний квадратичный радиус <r²>_ср? Классическая механика не может дать нам ответа. Мы должны вернуться назад и, во­оружившись квантовой механикой, начать все снова. Мы не можем знать, где именно находится электрон в атоме, а знаем лишь, что имеется вероятность его обнаружить в некотором месте. Если мы будем интерпретировать <r²>_ср как среднее значение квадрата расстояния от центра для данной вероят­ности распределения, то диамагнитный момент, даваемый квантовой механикой, определяется тем же самым выражением (34.17). Оно, разумеется, дает нам момент одного электрона. Полный же момент будет суммой по всем электронам в атоме. Удивительно, что и классические рассуждения и квантовая механика дают тот же ответ, хотя, как мы увидим дальше, «классические» рассуждения, которые приводят к (34.17), на самом деле несостоятельны в рамках самой классической ме­ханики.

Такой же диамагнитный эффект будет наблюдаться даже у атомов с постоянным магнитным моментом. При этом система тоже будет прецессировать в магнитном поле. Во время прецес­сии атома в целом он набирает небольшую дополнительную угловую скорость, а подобное медленное вращение приводит к маленькому току, который дает поправку к магнитному моменту. Это тот же диамагнитный эффект, но поданный по-другому. Однако на самом деле, когда мы говорим о парамагнетизме, нам не нужно заботиться об этой добавке. Если мы сначала подсчи­тали диамагнитный эффект, как это было сделано здесь, нас не должен беспокоить небольшой дополнительный ток, про­исходящий из-за прецессии. Он уже включен нами в диамаг­нитный член.

Дата добавления: 2015-08-20