Магнитные моменты и момент количества движения

Первая теорема, которую мы хотим доказать в классической механике, гласит: если электрон движется по круговой орбите (например, крутится вокруг ядра под действием центральных сил), то менаду магнитным моментом и моментом количества движения существует определенное соотношение. Обозначим через J момент количества движения, а через m — магнитный момент электрона на орбите. Величина момента количества движения равна произведению массы электрона на скорость и на радиус (фиг. 34.2). Он направлен перпендикулярно плоскости орбиты:

J =mvr. (34.1)

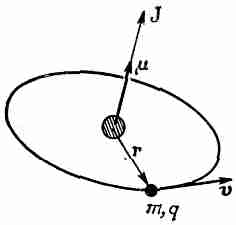
Фиг. 34.2. Для любой круговой орбиты магнитный момент m равен произведению q!2m на момент количества движения J.

(Хотя эта формула и нерелятивистская, но для атома она должна быть достаточно хороша, ибо у захваченного на орбиту элект­рона отношение v /c в общем случае равно по порядку величины е²/hc=1/137, или около 1%.)

Магнитный момент той же самой орбиты равен произведению тока на площадь (см. гл. 14, § 5, вып. 5). Ток равен положи­тельному заряду, проходящему в единицу времени через любую точку на орбите, т. е. произведению заряда q на частоту вра­щения. А частота равна скорости, поделенной на периметр орбиты, так что

I=q(v/2pr). Так как площадь равна pr², то магнитный момент будет

m =qvr/2 (34.2)

Он тоже направлен перпендикулярно плоскости орбиты. Таким образом, J и m имеют одинаковое направление:

m =(q/2m) J (орбиты). (34.3)

Их отношение не зависит ни от скорости, ни от радиуса. Для любой частицы, движущейся по круговой орбите, магнитный момент равен произведению q /2m на момент количества движе­ния. Для электрона, заряд которого отрицателен (обозначим его через - q_e),

m =-(q_e/2m) J (для электрона на орбите). (34.4)

Вот что получается в классической физике, и совершенно удивительно, что то же самое справедливо и в квантовой меха­нике. Это один из правильных выводов. Однако если развивать его дальше по пути классической физики, то вы натолкнетесь на такие места, где он даст неправильные ответы; разобраться же потом, какие результаты верны, а какие неверны, — целое дело. Уж лучше я сразу скажу, что в квантовой механике верно в общем случае. Прежде всего соотношение (34.4) остается вер­ным для орбитального движения; однако это не единственное место, где мы встречаемся с магнетизмом. Электрон, кроме того, совершает еще вращение вокруг собственной оси (подобное вращению Земли вокруг ее оси), и в результате этого вращения у него возникает момент количества движения и магнитный мо­мент. Но по чисто квантовомеханическим причинам (классиче­ское объяснение этого совершенно отсутствует) отношение m к J для собственного вращения (спина) электрона в два раза больше, чем для орбитального движения крутящегося элект­рона:

m =-(q_e/m) J (спин электрона). (34.5)

В любом атоме, вообще говоря, имеется несколько электро­нов, и его полный момент количества движения и полный маг­нитный момент представляют некоторую комбинацию спиновых и орбитальных моментов. И без каких-либо на то классических оснований в квантовой механике (для изолированного атома) направление магнитного момента всегда противоположно на­правлению момента количества движения. Отношение их не обязательно должно быть - q_e/m или - q_e/2m; оно расположено где-то между ними, ибо здесь «перемешиваются» вклады от спинов и орбит. Можно записать

' m =-g(q_e/2m) J (34.6)

где множитель g характеризует состояние атома. Для чисто орбитальных моментов он равен единице, для чисто спиновых равен 2, а для сложной системы, подобной атому, он расположен где-то между ними. Конечно, пользы от этой формулы не очень много. Она только говорит, что магнитный момент параллелен моменту количества движения, но может иметь любую величину. Тем не менее форма уравнения (34.6) все же удобна, ибо вели­чина g, называемая «фактором Ланде», есть безразмерная по­стоянная порядка единицы. Одна из задач квантовой меха­ники — предсказание фактора g для разных атомных состояний. Быть может, вам интересно знать, что происходит в ядрах атомов. Протоны и нейтроны в ядре движутся по своего рода орбитам и в то же время, подобно электронам, имеют спин. Маг­нитный момент снова параллелен моменту количества движе­ния. Только теперь порядок величины отношения магнитного момента к моменту количества движения для каждой из этих частиц будет таким, как можно было ожидать для протона, движущегося по кругу; при этом массу m в уравнении (34.3) нужно взять равной массе протона.

Поэтому для ядер обычно пишут (в скобках положительная величина)

m =g(q_e/2m_p) J (34.7)

где m_p— масса протона, а постоянная g, называемая ядерным g-фактором,— число порядка единицы, которое должно опре­деляться отдельно для каждого сорта ядер.

Другое важное отличие в случае ядер состоит в том, что g-фактор спинового магнитного момента протона не равен 2, как у электрона. Для протона g=2•(2,79). Крайне удивительно, что спиновый магнитный момент есть и у нейтрона и отношение этого магнитного момента к моменту количества движения равно 2•(-1,93). Другими словами, нейтрон в магнитном смысле не будет в точности «нейтральным». Он напоминает маленький маг­нитик и имеет такой же магнитный момент, как и вращающийся отрицательный заряд.

Дата добавления: 2015-08-20