Граничные условия

Все что мы делали до сих пор, было описанием трех волн; теперь нам предстоит выразить параметры отраженной и пре­ломленной волн через параметры падающей. Как это сделать?

Три описанные нами волны удов­летворяют уравнениям Максвелла в однородном материале, но, кро­ме того, уравнения Максвелла должны удовлетворяться и на границе между двумя материалами. Так что нам нужно сейчас посмотреть — что же происходит на самой границе. Мы най­дем, что уравнения Максвелла требуют, чтобы три волны опре­деленным образом согласовывались друг с другом.

Вот один из примеров того, что мы имеем в виду. Составляю­щая по оси у электрического поля Е должна быть одинакова по обеим сторонам границы. Это требуется законом Фарадея:

Ñ X E = д B / д t, (33.19)

в чем нетрудно убедиться. Рассмотрим для этого маленькую петлю Г, которая с обеих сторон охватывает границу (фиг. 33.4).

Фиг. 33.4. Граничное условие E_y2=E_y1, полученное из равенства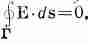

Согласно уравнению (33.19), криволинейный интеграл от Е по петле Г равен скорости изменения потока В через эту петлю:

Вообразите теперь, что прямоугольник очень узок, так что он замыкается в бесконечно малой области. Если при этом поле В остается конечным (нет никаких причин ему быть бесконечным!), то поток через эту область будет равен нулю. Таким образом, контурный интеграл от Е должен быть нулем. Если y-компоненты поля на двух сторонах границы равны Е _y1и Е _y2, а длина прямоугольника равна l, то мы получаем

E_y1l-E_y2l=0

или

Е_у1=Е_у2, (33.20)

как мы и ожидали. Это условие дает нам одно соотношение между полями в трех волнах.

Процедура нахождения следствий уравнений Максвелла на границе называется «определением граничных условий». Обычно она заключается в нахождении стольких уравнений типа (33.20), сколько возможно, и выполняется она с помощью рассмотрении маленьких прямоугольников, подобных Г на фиг. 33.4, или маленьких гауссовых поверхностей, охватываю­щих границу с двух сторон. Хотя это совершенно правильный способ рассуждений, он создает впечатление, что в различных физических задачах с границами нужно обращаться по-разному.

Как, например, в задаче о тепловом потоке через поверх­ность определить температуру на обеих прилежащих к ней сторонах? Конечно, вы вправе утверждать, что тепло, прите­кающее к границе с одной стороны, должно быть равно теплу, утекающему от нее с другой. Обычно это возможно и, вообще говоря, очень полезно находить граничные условия из такого рода физических рассуждений. Однако могут встретиться случаи, когда при работе над какой-то проблемой вам известны лишь уравнения и вы не можете непосредственно увидеть, какие же физические аргументы можно использовать. Так что, хотя в данный момент мы заинтересованы только в электромаг­нитных явлениях, где можно привести физические аргументы, я хочу научить вас методу, который можно применить в любой задаче: общему методу нахождения непосредственно из диффе­ренциальных уравнений того, что происходит на границе.

Начнем с выписывания всех уравнений Максвелла для ди­электрика, но на этот раз скрупулезно выписывая все компо­ненты:

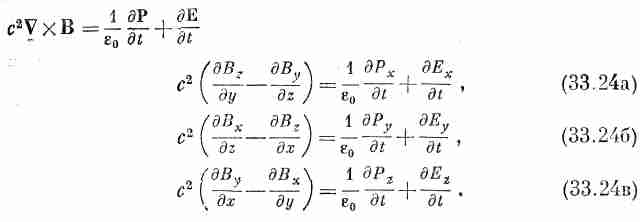
Эти уравнения должны быть справедливы как в области 1 (слева от границы), так и в области 2 (справа от нее). Мы уже выписывали решения в областях 1 и 2. Они должны удовлет­воряться и на самой границе, которую мы можем назвать об­ластью 3. Хотя обычно мы считаем границу чем-то абсолютно резким, на самом деле таких границ не бывает. Физические свойства, правда, изменяются очень быстро, но все же не беско­нечно быстро. Во всяком случае, мы можем считать, что между областями 1 и 2 изменение показателя преломления хотя и очень быстрое, но непрерывное. Это небольшое расстояние, на котором оно происходит, мы можем назвать областью 3. Подобный же переход в области 3 будут претерпевать и другие характери­стики поля, такие, как Р_х или Е_y и т. п. Однако дифферен­циальные уравнения должны удовлетворяться; именно следуя за дифференциальными уравнениями в этой области, мы придем к необходимым «граничным условиям».

Предположим, например, что у нас есть граница между вакуумом (область 1) и стеклом (область 2). В вакууме нечему поляризоваться, так что P ₁=0. А поляризация в стекле пусть равна Р₂. Между вакуумом и стеклом существует гладкий, но быстрый переход. Если мы проследим за какой-то компонентой Р, скажем Р_х, то она может изменяться так, как это показано на фиг. 33.5, а.

Фиг. 33.5. Поля в переходной об­ласти 3 между двумя различными материалами в областях 1 и 2.

Предположим теперь, что мы взяли первое из наших уравнений — уравнение (33.21). В него входит производ­ная от компонент Р по переменным х, у и z. Производные по у и r не очень интересны — в этих направлениях не происходит ничего замечательного. Но производная от Р_х по х в области 3 из-за быстрого изменения Р_х будет громадна. Производная дР_х/дх, как показано на фиг. 33.5,б, имеет на границе очень резкий пик. Если вы представите, что граница сжимается до еще более тонкой области, пик вырастет еще больше. Если для интересующих нас волн граница действительно резкая, то ве­личина дP/дx в области 3 будет больше, много больше любого вклада, который может получиться из-за изменения Р в сто­роне от границы, так что мы пренебрегаем любыми другими изменениями, за исключением происходящих на границе.

Но как теперь можно удов­летворить уравнению (33.21), если с правой стороны у нас возвышается огромный пик? Только если существует рав­ный ему громадный пик с другой стороны. Что-то и с левой стороны должно быть большим. Единственная воз­можность — это дЕ_х/дх, пос­кольку изменения в направ­лениях у и z в тех волнах, о которых мы только что упо­мянули, дают лишь малый эффект. Таким образом, -e ₀(дЕ_х/дх) должно быть, как это показано на фиг. 33.5,в, точной копией дP/дx. Получается

Если это уравнение проинтегрировать по х по всей области 3, то мы придем к заключению, что

e₀(Е_x2-Е_x1)=-(Р_x2-Р_x1). (33.25)

Другими словами, скачок e ₀Е_х при переходе от области 1 к об­ласти 2 должен быть равен скачку — Р_х.

Уравнение (33.25) можно переписать в виде

e₀E_x2+Р_x2=e₀E_x1+Р_x1; (33.26)

оно гласит, что величина (e₀E_x+Р_x) имеет равные значения как в области 2, так и в области 1. В таких случаях люди гово­рят, что величина ( e ₀Е_x+Р_х) непрерывна на границе. Таким образом, мы получили одно из наших граничных условий.

Хотя в качестве иллюстрации мы взяли случай, когда зна­чение Р ₁ равно нулю, ибо в области 1 у нас был вакуум, ясно, что те же аргументы приложимы для любого материала в этих двух областях, так что уравнение (33.26) верно в общем случае. Давайте перейдем к остальным уравнениям Максвелла и по­смотрим, что скажет нам каждое из них. Следующим мы возьмем уравнение (33.22а). У него нет производной по х, так что оно ничего нам не говорит. (Вспомните, что на границе сами поля не особенно велики. Только их производные по х могут стать столь огромными, что будут доминировать в уравнении.) Взгля­нем теперь на уравнение (33.22.б). Смотрите! Именно здесь у нас есть производная по х! С левой стороны имеется дE_z/дx. Пред­положим, что эта производная громадна. Но минуточку терпе­ния! С правой стороны нет ничего, способного потягаться с ней, поэтому Е_z не может иметь скачка при переходе из области 1 к области 2. [Если бы это было так, то с левой стороны уравне­ния (33.22а) мы бы получили скачок, а с правой — его не было бы, и уравнение оказалось бы неверным.] Итак, мы получили новое условие:

E_я2=E_я1. (33.27)

После тех же самых рассуждений уравнение (33.22в) дает

E_y2=E_y1. (33.28)

Последний результат в точности совпадает с полученным с по­мощью контурного интеграла условием (33.20).

Перейдем к уравнению (33.23). Единственное, что может дать пик,— это дВ_х/дх. Но справа опять нет ничего, способного противостоять ему; в результате мы заключаем, что

B_x2=B_x1. (33.29)

И, наконец, последнее из уравнений Максвелла! Уравнение (33.24а) ничего не дает, ибо там нет производных по х. В урав­нении (33.236) — одна производная: — с²(дВ_z/дх), но ей снова нечего противопоставить с другой стороны равенства, поэтому мы получаем

B_z1=B_z2. (33.30)

Совершенно аналогично второе уравнение, которое дает

B_y1=B_y2. (33.31)

Итак, последние три условия говорят нам, что В₂=В₁.

Хочу здесь подчеркнуть, что такой результат получен только потому, что по обеим сторонам границы мы взяли немагнитный материал, вернее, потому, что магнитным эффектом этих мате­риалов мы можем пренебречь. Обычно это вполне допустимо для большинства материалов, за исключением ферромагнетиков. (Магнитные свойства материалов мы будем рассматривать в по­следующих главах.).

Наша программа привела нас к шести соотношениям между полями в областях 1 и 2. Все они выписаны в табл. 33.1. Их можно использовать для согласования волн в двух областях.

Таблица 33.1 • граничные условия на поверхности ДИЭЛЕКТРИКА

(Поверхность расположена в плоскости yz.)

Однако я хочу отметить, что идея, которую мы только что использовали, будет работать в любой физической ситуации, где у вас есть дифференциальные уравнения и требуется найти решение в области, пересекаемой резкой границей, по обе стороны которой некоторые из физических свойств различны. Для наших теперешних целей было бы легче получить те же самые уравнения с помощью рассуждений о потоках и циркуляциях на границе. (Проверьте, можно ли подобным путем по­лучить те же самые результаты.) Однако теперь вы знаете метод, который будет хорош, даже когда вы попали в затруднительное положение и не видите простых физических соображений от­носительно того, что происходит на границе. Вы можете просто воспользоваться дифференциальными уравнениями.

Дата добавления: 2015-08-20