Циркуляция

В начале предыдущего параграфа мы видели, что если у нас есть безвихревая несжимаемая жидкость, то поток удов­летворяет следующим двум уравнениям:

Ñ•v=0, ÑXv=0. (40.19)

Эти уравнения аналогичны уравнениям электростатики или магнитостатики в пустом пространстве. При отсутствии зарядов дивергенция электрического поля равна нулю, а ротор электро­статического поля всегда равен нулю. Ротор магнитного поля равен нулю при отсутствии токов, а дивергенция магнитного поля всегда равна нулю. Следовательно, уравнения (40.19) имеют такие же решения, как и уравнения для Е в электро­статике или уравнения для В в магнитостатике. Фактически в гл. 12, § 5 (вып. 5), мы уже решили задачу об обтекании сферы потоком в качестве электростатического аналога. Электростатическим аналогом является однородное электриче­ское поле плюс поле диполя, причем поле диполя подбирается таким, чтобы скорость потока, нормальная к поверхности сферы, была равна нулю. Задачу об обтекании цилиндра можно решить таким же способом, выбрав подходящее направление диполя относительно однородного потока. Эти решения спра­ведливы в тех случаях, когда скорость жидкости на больших расстояниях постоянна как по величине, так и по направлению. Они изображены на фиг. 40.11,а.

Фиг. 40.11. Обтекание цилиндра идеальной жидкостью (а), циркуля­ция вокруг цилиндра (б) и cyпepрозuция случаев а и б (в).

Задача об обтекании цилиндра имеет и другое решение, когда условия таковы, что поток на больших расстояниях движется по окружности вокруг цилиндра. Тогда поток будет круговым повсюду (фиг. 40.11,6). У такого потока есть цирку­ляция вокруг цилиндра, хотя ÑXv в жидкости остается нулем. Но как циркуляция может существовать без ротора?

У нас есть циркуляция вокруг цилиндра, ибо криволинейный интеграл от v по замкнутой пет­ле, охватывающей цилиндр, не равен нулю. В то же время криволинейный интеграл от v по любому замкнутому пути, который не охватывает цилинд­ра, будет нулем. Аналогичные вещи встречались нам и рань­ше, когда мы определяли маг­нитное поле вокруг проводника. Ротор В был нулем вне провода, хотя криволинейный интеграл от В по пути, охватывающему провод, не исчезает. Поле скоростей в безвихревой циркуля­ции вокруг цилиндра в точности такое же, как и магнитное поле вокруг провода. Для кругового пути с центром, совпадаю­щим с центром цилиндра, криволинейный интеграл от скорос­ти равен

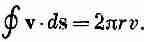
Для безвихревого потока интеграл не должен зависеть от r. Обозначим его через постоянную С и получим

где v — тангенциальная скорость, а r — расстояние от оси. Существует очень хороший способ демонстрации циркуля­ции жидкости в трубе. Вы берете прозрачный цилиндрический резервуар с трубкой в центре дна. Наполняете его водой, немного раскручиваете ее палочкой и вынимаете пробку из отводной трубы. И получаете тот красивый эффект, который показан на фиг. 40.12.

Фиг. 40.12. Вода с циркуляцией вытекает из резервуара.

(Подобное явление вы наверняка много раз видели в ванне!) Хотя вначале вы и создали некоторую угловую скорость w, она из-за вязкости вскоре затухает и поток становится безвихревым. Однако ка­кая-то циркуляция вокруг трубки все же остается.

Из теории можно вычислить форму по­верхности воды в цилиндре. По мере того как частицы движутся внутрь, они набирают скорость. Согласно уравнению (40.20), тан­генциальная скорость увеличивается как 1/r — просто благодаря закону сохранения момента количества движения, как у фигуриста, при­жавшего руки к телу. Радиальная скорость тоже возрастает как 1/r. Если пренебречь тангенциальным движением, то полу­чится, что вода идет внутрь по радиусу к отверстию, а из урав­нения Ñ•v=0 следует, что радиальная скорость пропорцио­нальна 1/r. Таким образом, полная скорость тоже возрастает как 1/г и вода идет по спирали Архимеда. Поверхность вода — воздух целиком находится под атмосферным давлением, так что, согласно уравнению (40.14), она должна обладать свойством

gz+¹/₂mv²= const.

Ио здесь v пропорционально 1/r, поэтому форма поверхности будет такой:

Обратите внимание на одну интересную особенность, кото­рая наблюдается в случае несжимаемого безвихревого потока (в общем случае ее нет): если у нас есть какое-то одно решение и какое-то второе решение, то сумма их тоже будет решением. Это справедливо потому, что уравнения (40.19) — линейные. Полный же набор гидродинамических уравнений, т. е. урав­нений (40.8) — (40.10), не линеен, а это уже совсем другое дело. Однако для безвихревого потока вокруг цилиндра мы можем сложить один поток (фиг. 40.11,а) и другой поток (фиг. 40.11,б) и получить новый вид потока (фиг. 40.11,в). Этот новый поток особенно интересен. Скорость потока на верхней стороне цилиндра оказывается больше, чем на нижней, так что когда на циркуляцию вокруг цилиндра налагается чистый горизонтальный поток, то возникнет действующая на цилиндр вертикальная сила; она называется подъемной силой. Разумеется, если циркуляция отсутствует, то в соответствии с нашей теорией «сухой» воды для любого тела суммарная сила обращается в нуль.

Дата добавления: 2015-08-20