Гидростатика

Кого не пленяет течение жидкости, кто не любуется течением воды! Все мы в детстве любили плескаться в ванне или возиться в гряз­ных лужах. Став постарше, мы восхищались плавным течением реки, водопадами и водо­воротами; мы любуемся ими, рядом с твердыми телами они кажутся нам почти одушевленными.

Предметом этой и следующей глав будет пове­дение жидкости, столь неожиданное и столь интересное. Попытки ребенка преградить путь маленькому ручейку, текущему по улице, и его удивление перед тем, как вода умудряется все же пробить себе дорогу, напоминает наши мно­голетние попытки понять механизм течения жидкости. Мы пытались мысленно преградить путь воды дамбой, т. е. получить законы и урав­нения, которые описывают поток. Рассказу об этих попытках и посвящена настоящая глава. А в следующей главе мы опишем тот уникаль­ный способ, с помощью которого вода проры­вает дамбу и ускользает от нас, не дав нам понять ее.

Я предполагаю, что элементарные свойства воды вам уже известны. Основное свойство, которое отличает жидкость от твердого тела, заключается в том, что жидкость не способна сдерживать ни мгновение напряжения сдви­га. Если к жидкости приложить напряжение сдвига, то она начинает двигаться. Густые жидкости, подобные меду, движутся менее легко, чем жидкости типа воды или воздуха. Мерой легкости, с которой жидкость течет, является ее вязкость. В этой главе мы рас­смотрим такие случаи, когда эффектом вяз­кости можно пренебречь. А эффекты вязкости отложим до следующей главы.

Начнем с рассмотрения гидростатики, т. е. теории непод­вижной жидкости. Если жидкость находится в покое, то на нее не действуют никакие сдвиговые силы (даже в вязкой жидкости). Поэтому закон гидростатики заключается в том, что напряже­ния внутри жидкости всегда нормальны к любой ее поверх­ности. Нормальная сила на единичную площадь называется давлением. Из того факта, что в неподвижной жидкости нет сдвигов, следует, что напряжение давления во всех направле­ниях одинаково (фиг. 40.1).

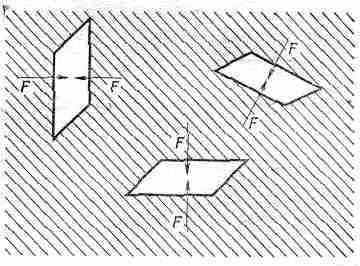
Фиг. 40.1. В неподвижной жидкости сила, действующая на единичную площадь любой поверхности, перпендикулярна этой поверхности и при любых ориентациях поверхности одна и та же.

Займитесь самостоятельно доказа­тельством того, что если на любой плоскости в жидкости сдвиг отсутствует, то давление во всех направлениях должно быть одинаковым.

Давление в жидкости может изменяться от точки к точке. Так, в неподвижной жидкости на поверхности Земли давление будет изменяться с высотой из-за веса жидкости. Если плот­ность жидкости r считается постоянной и давление на некотором нулевом уровне обозначено через р₀ (фиг. 40.2), то давление на высоте h над этой точкой будет р=р₀ -rgh, где g — сила тяжести единицы массы.

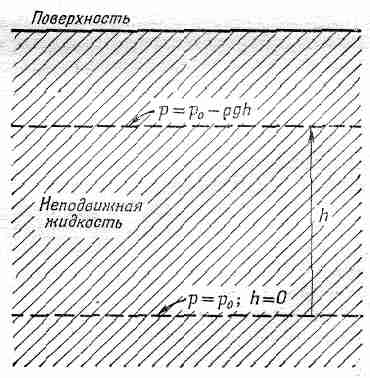
Фиг. 40.2. Давление в не­подвижной жидкости.

Комбинация р +r gh в неподвижной жидкос­ти остается постоянной. Вы знаете это соот­ношение, но теперь мы получим более об­щий результат, где на­ше соотношение будет лишь частным случа­ем. Возьмем маленький кубик воды. Какая сила действует на него в результате оказываемого давления? Поскольку давление в любом месте во всех направлениях одинаково, то полная сила, действующая на единицу объема, может быть обусловлена только изменением давления от точки к точке. Предполо­жим, что давление изменяется в направлении оси х, и выберем направления других осей координат параллельно ребрам ку­бика. Давление на грань с координатой х дает силу pDy/Dz (фиг. 40.3), а давление на грань с координатой х +D х дает силу—[ р+(др/дх) D х ] D y D z, так что результирующая сила равна - (др/дх) D x DyzDz.

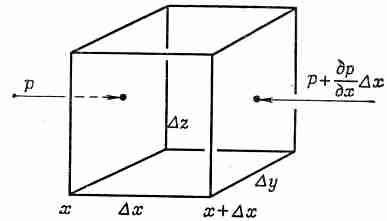
Фиг. 40.3. Полная сила давления, действующая на куб, составляет -Ñp на единицу объема.

Если же мы учтем остальные пары граней куба, то нетрудно убедиться, что сила давления на единичный объем равна -Ñ p. Если вдобавок есть еще и другие силы, наподобие силы тяжести, то давление при равновесии должно компенсироваться ими.

Разберем случай, когда такие дополнительные силы можно описать потенциальной энергией, наподобие силы тяжести. Обозначим через j потенциальную энергию единицы массы. (Для притяжения, например, j просто равно gz.) Сила, дейст­вующая на единичную массу, задаётся через потенциал j выражением -Ñj, а если плотность жидкости равна r, то на единицу объема будет действовать сила -rÑj. В состоянии равновесия эта действующая на единичный объем сила в сумме с силой давления должна давать нуль:

-Ñp-rÑj=0. (40.1)

Это и есть уравнение гидростатики. В общем случае оно не имеет решения. Если плотность изменяется в пространстве каким-то произвольным образом, то нет возможности уравновесить все силы и жидкость не может находиться в состоянии статиче­ского равновесия. В ней возникнут разные конвекционные потоки. Это видно прямо из уравнения, ибо член с давлением представляет чистый градиент, тогда как второй член из-за плотности r не может быть им. И только когда величина r по­стоянна, потенциальный член становится чистым градиентом.

Решение уравнения в этом случае имеет вид

р+rj=const.

Другая возможность, допускающая состояние равновесия,— это когда r зависит только от р. Однако на этом мы расста­немся с гидростатикой, ибо она не так интересна, как дви­жущаяся жидкость.

Дата добавления: 2015-08-20