
Читайте также:
|
В двух численных экспериментах использовались геометрические параметры расчетной зоны, приведенные в таблицt 7.1, а в таблице 7.1 – параметры газового потока гексафторида урана.
Таблица 7.1
Параметры расчетной области при обтекании прямоугольного выступа эйлеровым газом
| № эксперимента | 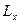 ,
м ,
м
| 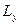 ,
м ,
м
| 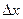 ,
м ,
м
| 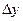 ,
м ,
м
| 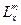 ,
м ,
м
| 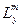 ,
м ,
м
|  , м , м
|
| 1,5 | 0,03 | 0,05 | 0,45 | 0,75 | 0,6 | ||
| 1,5 | 0,025 | 0,05 | 0,375 | 0,75 | 2,5 |
Таблица 4.2
Параметры газа при обтекании прямоугольного выступа эйлеровым газом
| № эксперимента | 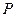 ,
Па ,
Па
| 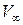 ,
м/с ,
м/с
| 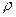 ,
кг/м3 ,
кг/м3
| 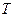 ,
К ,
К
| 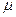 ,
кг/моль ,
кг/моль
|
| 0,188 | 0,352 | ||||
200 (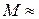 2) 2)
| 0,188 | 0,352 |
На рис. 7.29 приведено полученное в численном эксперименте № 1 поле скоростей, а на рис. 7.30 – поле давления. При обтекании выступа эйлеровым газом при заданных условиях образуется две зоны циркуляции: сверху над выступом и справа от выступа. На рис. 7.30 можно видеть, что в тех местах, где возникают зоны циркуляции потока (рис. 7.29), давление заметно уменьшается. И напротив, слева от выступа, где поток набегающего газа «упирается» в стенку, давление возрастает.
В увеличенном масштабе эти зоны вихревого движения изображены над выступом на рис. 7.31, а за выступом на рис.7.32. Как видно на рис. 7.31, в отсутствии сил вязкости вблизи твердой стенки над выступом поток гексафторида урана циркулирует в двух вихрях: по набегающему потоку в передней части по часовой стрелке и против направления набегающего потока в задней части против часовой стрелки, в которую наблюдается заброс среды из глобального вихря за выступом, как видно на рис. 7.31 и 7.32.
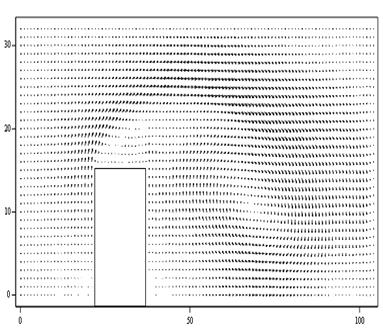
Рис. 7.29. Распределение скоростей индивидуальных частиц
в расчетной области (эксперимент № 1)
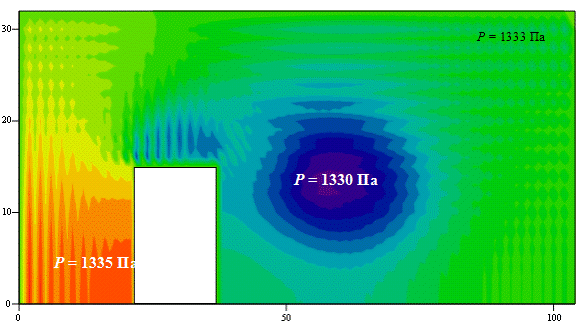
Рис. 7. 30. Распределение давления в расчетной области
(эксперимент № 1)
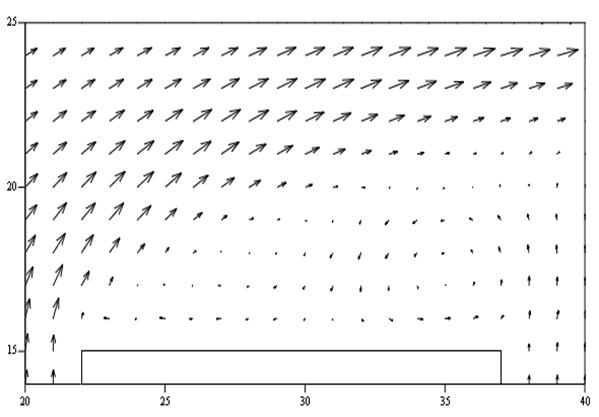
Рис. 7.31. Поле скоростей над верхней поверхностью выступа
(эксперимент № 1)
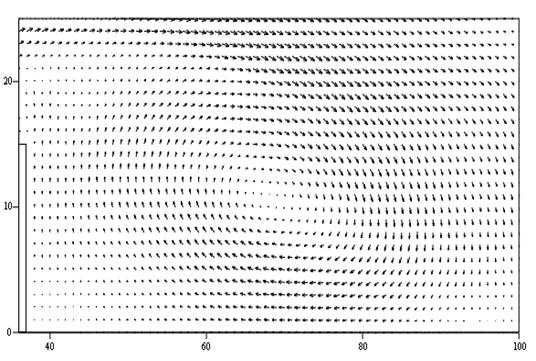
Рис. 7.32. Глобальный вихрь за выступом
При обтекании прямоугольного выступа сверхзвуковым потоком газа (эксперимент №2 в табл. 7.1, 7.2) образуется ударная волна перед выступом (рис 7.33 и 7.34). На рисунках видно, что перед пластинкой образуется ударная волна, давление в которой почти в 5 раз превышает давление в набегающем потоке, а за пластинкой образуется обширная разреженная зона, давление в которой в 1.5 раза меньше давления в набегающем потоке.
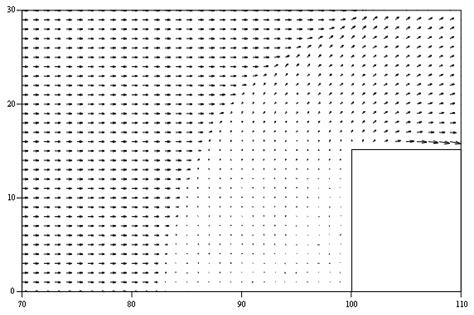
Рис. 7.33. Поле скоростей перед выступом (эксперимент № 2)
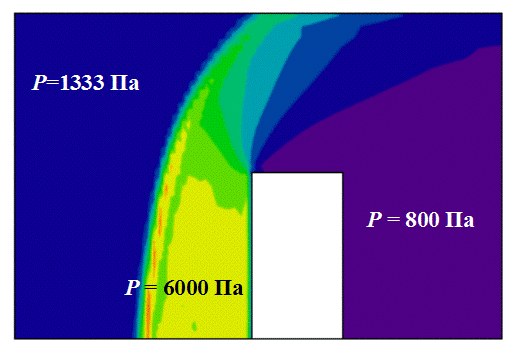
Рис. 7.34. Ударная волна в сверхзвуковом потоке идеального газа
при обтекании выступа (эксперимент № 2)
Таким образом, при обтекании выступа сверхзвуковым потоком идеального газа перед ним возникает ударная волна – скачок уплотнения плотности. Во фронтальной и кормовой областях поля течения возникает разность давлений, которая тем больше, чем выше скорость набегающего потока. Эта разность давлений является источником возрастания энтропии в сверхзвуковом потоке идеального газа.
ЛИТЕРАТУРА:
1. Белоцерковский О.М. Численное моделирование в механике сплошных сред.- М.: Наука, 1984.
2. Марчук Г.И. Методы вычислительной математики.- М.: Наука, 1977.
3. Самарский А.А. Теория разностных схем.- М.: Наука, 1977.
4. Бёрд Дж. Молекулярная газовая динамика.- М.: Мир, 1965.
5. Пирумов У.Г., Росляков Г.С. Численные методы газовой динамики.- М.: Высш. Шк., 1987.
6. Бабаков А.В. Численное моделирование некоторых задач аэрогидродинамики.-М.: ВЦ АН СССР, 1986, с. 56.
Дата добавления: 2015-08-03; просмотров: 35 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Этапы вычислительного цикла | | | Идеальная бывшая |