Численное дифференцирование

Если функция задана в точках , то естественным способом вычисления ее производной является дифференцирование интерполяционного многочлена. Интерполяционный многочлен Лагранжа (7.10.1) приближает функцию с погрешностью , поэтому замена -ой производной -ой производной полинома Лагранжа порождает погрешность

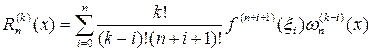, (7.10.15)

. (7.10.16)

Рассмотрим случай при равноотстоящих узлах , 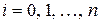. Легко показать, что в этом случае выражения для вычисления производной будут выглядеть так:

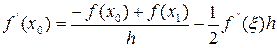, (7.10.17)

(7.10.18)

Эти формулы называют односторонними аппроксимациями первой производной функции соответственно вперед и назад; они имеют погрешность , т.е. аппроксимируют первую производную с первым порядком точности.

Формулы для производных при 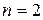имеют вид:

,

(7.10.19)

Порядок аппроксимации этих формул равен двум.

Для более детального ознакомления с формулами интерполирования, численного интегрирования и дифференцирования и другими аспектами численных методов можно порекомендовать [3, 5].

Дата добавления: 2015-08-03