Описание метода потоков

В данном разделе будут изложены общие принципы построения конечно-разностных схем метода потоков, разработанного Л.И. Севериновым и А.В. Бабаковым, [6].

В переменных поля метод порождает явную разностную схему, которая является условно – устойчивой и условно монотонной. Схема в силу способа ее построения является консервативной по массе, по составляющим импульса и полной энергии.

Решение задачи ищется в области L, границы которой образованы контуром обтекаемого тела и некоторой достаточно удаленной от тела замкнутой поверхностью 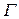. Разобьем эту область на малые фиксированные в пространстве объемы-ячейки 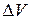. Каждую ячейку будем характеризовать массой 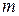, составляющими импульса 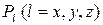и полной энергией газа, находящегося в .

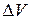Зная значения 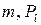и Е можно вычислить средние для данной ячейки величины плотностей распределения перечисленных количеств:

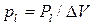, , . (7.11.1)

где 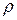- массовая плотность газа; 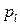- i – компонента плотности распределения импульса; - плотность распределения полной энергии.

Полученные значения относятся к некоторым характерным точкам объемов 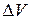(как правило, берется геометрический центр).

От функци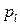й и 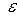легко перейти к общепринятым переменным поля – составляющим 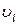вектора скорости 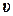и удельной внутренней энергии газа :

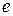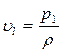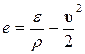, . (7.11.2)

Указанные значения приписываются тем же характерным точкам ячеек 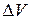, к которым уже отнесены плотности распределения.

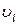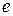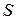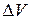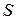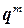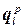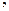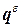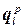Используя некоторые процедуры интерполирования и численного дифференцирования, определим значения переменных поля и первых производных от и на границах ячеек . Знания этих величин достаточно для того, чтобы вычислить на векторы плотностей потоков массы , составляющих импульса единичную и энергии газа , где - вектор плотности потока импульса через площадку перпендикулярную оси .

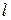Выпишем теперь законы сохранения массы, импульса, и энергии, определяющие фундаментальные свойства среды, в виде поверхностных интегралов от векторов плотностей потоков 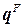по поверхности 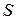каждой ячейки 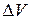. В общем (нестационарном случае) эти законы имеют вид:

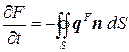, (7.11.3)

где 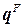- вектор плотности потока величины 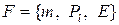, 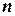- единичный вектор внешней к 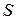нормали. Векторы плотностей потоков 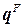определяются на поверхности 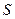переменными газодинамического поля и их производными и плотностями распределения. Уравнения (7.11.3) справедливы для произвольного объема, и естественно требовать их выполнения для минимального объема-ячейки разностной сетки.

Естественными дополнительными условиями для системы (7.11.3) являются значения векторов плотностей потоков каждого из количеств на поверхностях, ограничивающих область интегрирования. Вид этих условий зависит от рассматриваемой физической задачи.

Таким образом, сформулированная выше задача сводится теперь к следующему: необходимо определить значения переменных газодинамического поля и плотностей распределения в характерных точках объема 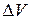так, чтобы уравнения (7.11.3) выполнялись с требуемой точностью для каждого элементарного объема.

При численном решении интегралы в (7.11.3) вычисляются по квадратурной формуле

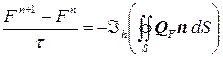, (7.11.4)

где векторы плотностей потоков 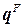определяются по значениям плотностей распределения и переменных газодинамического поля в характерных внутренних точках объемов 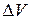. Величины 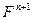вычисляются с погрешностью . Оператор 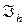определяет конечно – разностное представление интеграла по некоторой квадратурной формуле, зависящей от - шага расчетной сетки.

Уравнения (7.11.4), выписанные для каждой аддитивной характеристики среды 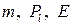во всех элементарных объемах (ячейках), составляют систему нелинейных алгебраических уравнений относительно переменных газодинамического поля в одной точке элементарного объема (ячейки) 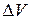. Система уравнений (7.11.4) вместе с соотношениями (7.11.1), (7.11.2), дополненная уравнением состояния и граничными условиями, является замкнутой.

Остановимся на отличительных чертах рассматриваемой численной модели. Все переменные в (7.11.3) естественно разделяются на две группы: первую – переменные газодинамического поля (составляющие вектора скорости 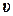, давление 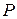, температура 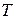) и вторую – переменные плотности распределения количеств - потоки, для которых сформулированы законы сохранения (7.11.3).

Переменные первой группы являются в физическом смысле активными, интенсивными и имеют локальный характер. В их терминах формулируется причинная часть законов переноса. В терминах переменных второй группы формулируется количественная часть законов переноса, т.е. следствие. Переменные этой группы, называемые экстенсивными, представляют собой плотности распределения аддитивных характеристик среды. Например, поток импульса определяется плотностью распределения импульса (экстенсивная переменная), величинами газодинамического поля и их производными (интенсивные переменные) и т.д.

В соответствии с разным физическим смыслом переменных кажется естественным, что их определение на границах 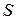элементарного объема 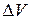также должно быть различным.

В методе потоков плотности распределения аддитивных характеристик среды вычисляются с учетом направления вектора скорости, что приводит к использованию несимметричных аппроксимационных формул. Направление вектора скорости учитывается в том смысле, что плотность распределения любой аддитивной характеристики среды в некоторой точке определяется плотностями распределения в точках, лежащих от рассматриваемой точки против течения. Наличие конвективного переноса делает пространственные направления неравнозначными, что естественно учитывать при конструировании разностных схем.

Переменные же газодинамического поля и их производные (в тензоре вязких напряжений и законе теплопроводности) определяются по симметричным формулам. На аппроксимацию переменных газодинамического поля накладывают ограничения и другие законы механики.

Таким образом, если при разностном представлении уравнений (7.11.3) задаются законы механики (исходя из которых и получаются уравнения Навье - Стокса), то естественно ожидать, что между областями зависимости разностных и дифференциальных уравнений будет соблюдаться правильное соответствие. В представлении (7.11.4) обычно используется равномерная пространственная сетка.

Переход к интегральным законам сохранения (7.11.3) требует, по существу, аппроксимации производных на единицу меньшего порядка по сравнению с прямыми методами численного решения уравнений Навье – Стокса.

Нетрудно заметить, что по своей сущности метод потоков обладает свойством консервативности по массе, импульсу и полной энергии на каждом временном слое [6], причем консервативность здесь имеет место как локально (для каждой ячейки разностной сетки), так и интегрально, т.е. для всей расчетной области. Как следует из (7.11.3), свойство консервативности обеспечивается тем, что данный подход основан на разностной аппроксимации законов сохранения, выписанных для каждой ячейки расчетной сетки в терминах поверхностных интегралов от векторов плотностей потоков 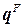, т.е. закон сохранения используется в форме, справедливой для произвольного объема газа.

Действительно, при решении конкретной задачи поверхностные интегралы в (7.11.4) вычисляются на отдельных участках поверхностей 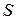, являющихся границами между двумя соседними объемами 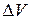. В зависимости от направления векторов потоков значения 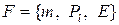изменяются (в одних ячейках увеличиваются, а в других уменьшаются) на величины, определяемые потоками массы, импульса и полной энергии через совпадающие участки границы. Такой способ вычислений не может привести с точностью до ошибок округления к потере или образованию количеств 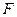из-за вычислительных процедур, что и свидетельствует о консервативности. Здесь проводится перенос (а, следовательно, и аппроксимация) «комплексов» функций – плотностей распределения количеств массы, импульса и энергии, что отвечает физике явления. В основу указанного подхода заложена общность факторов переноса (откуда и название – метод потоков). Анализ схемы с точки зрения выполнения законов сохранения представляется важным, так как известно, что расчетная схема дает наиболее точные результаты, когда она строго сохраняет те величины, которые сохраняются в рассматриваемом физическом процессе.

7.11.3. Конечно – разностные схемы метода потоков

Рассмотрим принципы построения конечно – разностных схем метода потоков. Будем искать решение задачи внешнего обтекания двумерного прямоугольного выступа эйлеровым газом.

Дата добавления: 2015-08-03