|
Читайте также: |
Пусть необходимо найти распределение газодинамических параметров газа при обтекании бесконечного прямоугольного выступа потоком набегающего газа (см. рис. 7.27). В связи с тем, что выступ является бесконечным по одной из осей, нет необходимости решать трехмерную задачу. Достаточно выделить отрезок выступа единичной длины и решать для него двумерную задачу. Силой тяжести можно пренебречь. Решение такой задачи будем искать в области между обтекаемым выступом и границей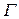 
, достаточно удаленной от самого выступа для уменьшения погрешности, вызванной ограниченностью расчетной области L.
Согласно п. 7.11.2 разобьем расчетную область на прямоугольные ячейки с линейными размерами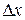 
и 
. Взяв по оси абсцисс 
, а по оси ординат 
ячеек, получим, что линейные размеры расчетной области равны 
. Стороны ячейки образованы линиями
, 
. (7.11.5)
В качестве характерных внутренних точек объемов, к которым будем относить переменные поля, выберем на плоскости 
точки с координатами
, 
. (7.11.6)
Рис. 7.27. Расчетная область поля течения
- расчетная область; 
- граница расчетной области; 
- скорость набегающего потока; 
- расчетная ячейка с индексами 
и 
; 
- граница между ячейками и 
; 
- линейные размеры расчетной области; 
- линейные размеры обтекаемого тела; 
- расстояние от левой границы расчетной области до левого края выступа.
Через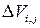 
будем обозначать объем, содержащий точку 
.
Вычисление потоков соответствующих величин в (7.11.4) осуществляется через четыре участка внешней поверхности 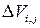, которые обозначим соответственно через 
, так что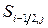 
разделяет ячейк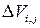и и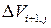 
и т. д. с использованием квадратурной формулы прямоугольников с центральной узловой точкой. Координаты узла на границе 
, например, равны
. (7.11.7)
Такая квадратурная формула требует определения в узловых точках переменных поля и первых производных от составляющих вектора скорости и удельной внутренней энергии. Эти величины в дальнейшем будем обозначать с помощью полуцелых индексов, например: 
на .
В предлагаемом варианте метода потоков в основу вычислительного алгоритма положены нестационарные уравнения (7.11..3). Если в момент времени 
известны значения 
, где 
- шаг интегрирования по времени, то в момент 
эти величины с погрешностью 
могут быть вычислены следующим образом:
, 
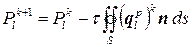, (7.11.8) 
.
Дата добавления: 2015-08-03; просмотров: 37 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Описание метода потоков | | | Обтекание прямоугольного выступа эйлеровым газом |