Обтекание прямоугольного выступа эйлеровым газом

Будем искать решение задачи обтекания выступа эйлеровым газом при условии постоянства температуры в системе. Это позволит не вычислять поток внутренней энергии через границы ячейки, т.к. внутренняя энергия в таком случае постоянна. Таким образом, на каждом шаге расчета для каждой стороны ячейки необходимо вычислять плотность потока массы 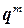и две компоненты плотности потока импульса 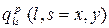. Запишем выражения для плотности потока массы и импульса для эйлерова газа:

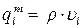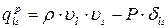, . (7.11.9)

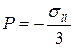. (7.11.10)

Здесь Р – гидростатическое давление; 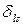– символ Кронекера. Следует заметить, что в литературе встречаются выражения (7.11.9), в которых перед давлением стоит знак (+). Такое различие связано с тем, что можно по разному понимать давление: как силу, действующую на сжатие (-), или как силу, действующую на растяжение (+) элементарного объема при выводе выражения для плотности потока импульса.

Необходимо записать конечно–разностные выражения для (7.11.9) и (7.11.10). Для примера запишем эти выражения для площадки 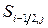. Они имеют тот же вид, что и (7.11.9) и (7.11.10), только параметры поля заменяются на вычисленные значения на границе между ячейками:

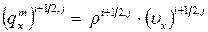, (7.11.11)

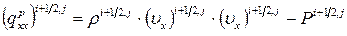, (7.11.12)

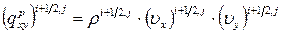. (7.11.13)

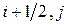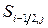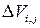Индексы означают, что соответствующие параметры вычисляются на границе между и 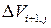. Теперь распишем формулы для вычисления каждого параметра из (7.11.11-13). Согласно соображениям, приведенным в п. 7.11.3.2, массовую плотность необходимо аппроксимировать по несимметричной формуле, учитывающей направление потока:

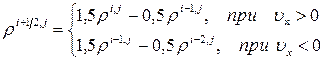(7.11.14)

Скорости на границе ячейки вычисляются по симметричным формулам:

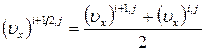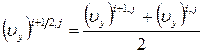, . (7.11.15)

Давление 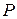можно получить из уравнения состояния идеального газа, записанного для конечно – разностных аналогов параметров газа:

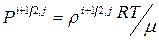, (7.11.16)

где 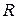- универсальная газовая постоянная; 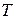- температура системы; 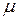- молярная масса газа.

Следует заметить, что существует определенная неоднозначность выбора аппроксимаций для термодинамических параметров. Причем некоторые из этих аппроксимаций являются аналогичными с точки зрения точности. Предпочтительность каких-то конкретных вариантов необходимо определять опытным путем. Например, численные эксперименты показали, что с точки зрения устойчивости расчета в (7.11.16) для определения давления лучше использовать среднее арифметическое плотностей граничащих ячеек, а не плотность, вычисленную по формуле (7.11.14). Формулы (7.11.11-16) имеют второй порядок точности.

Аналогичным способом записываются выражения для оставшихся трех границ ячейки.

Необходимо остановиться на процедуре задания граничных условий. Граничные условия можно разделить на два типа:

1. граничные условия на внешней границе;

2. граничные условия на твердом теле.

Необходимость задания первого типа условий вызвана тем, что расчетная область ограничена. На внешней границе 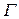расчетной области должны быть заданы условия, не оказывающие существенного влияния на решение вблизи обтекаемого тела. Внешние границы расчетной области должны располагаться достаточно далеко от обтекаемого тела. Потому что граничные условия оказывают влияние на решение вблизи границы. Данное обстоятельство вызвано тем, что условия на внешней границе выбираются, исходя из параметров набегающего потока. Если же внешняя граница расположена близко к обтекаемому телу, то возмущения поля течения, вызванные наличием обтекаемого тела, не успевают затухнуть, и возникает большой перепад параметров у внешней границы, что нарушает картину течения и вносит дополнительную погрешность. Можно использовать различные варианты организации этих условий. Например, вводить слой приграничных ячеек и для обеспечения отсутствия скачкообразного изменения параметров вычислять их значение как среднее между условиями набегающего потока и ближайшей ячейкой внутри области, или аппроксимировать с различной точностью изменения параметров в соседних ячейках внутри области и экстраполировать их на приграничные ячейки. Как правило, наиболее удачным является выбор комбинации различных вариантов организации граничных условий. К примеру, с «наветренной» (см. рис. 7.) стороны выступа для приграничных ячеек можно использовать усреднение между соседними ячейками внутри области и условиями набегающего потока. С «подветренной» стороны можно экстраполировать на приграничные ячейки параметры ячеек, расположенных внутри расчетной области. Данный способ учитывает преимущественное направление возмущений потока. С «наветренной» стороны эти возмущения «сдуваются» струей набегающего потока (поэтому в граничных условиях для этой стороны и фигурируют условия набегающего потока), а с «подветренной» стороны возмущенный поток газа движется в сторону правой границы (поэтому проводится экстраполяция изнутри расчетной области). Несмотря на все вышесказанное можно использовать вариант для «наветренной» стороны и для всей области. Просто необходимо будет отодвинуть правую границу дальше от тела на такое расстояние, где «след», оставляемый телом, исчезает, и поток можно считать невозмущенным.

Второй тип условий отражает физическую модель взаимодействия газа с обтекаемым телом. Эти граничные условия делятся на два вида:

1. условие непротекания,

2. условие прилипания.

Условие непротекания означают, что газ не может попасть в твердое тело и накапливаться с течением времени на его поверхности, и выражается в равенстве нулю нормальной к поверхности тела компоненты скорости газа. Условие прилипания означают, что на границе с твердым телом газ полностью тормозится и имеет нулевую скорость. В этом случае вектор скорости газа на границе газ - твердое тело равен нулю. Условие прилипания бессмысленно формулировать для невязкого (эйлеровского) газа, т.к. в этом случае отсутствует механизм, который позволил бы другим слоям газа (не прилегающим к поверхности) «чувствовать» торможение около твердого тела. В методе потоков для обеспечения условий на границе с твердым телом необходимо задавать плотности потоков импульса.

Дата добавления: 2015-08-03