Подключение неразветвленнои цепи с индуктивным, резистивным и емкостным элементами к источнику постоянной ЭДС

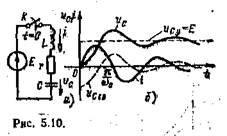
Для неразветвленной цени с индуктивным, резистнвным и емкостным элемен­тами и источником постоянной ЭДС (рис. 5. 10, а) дифференциальное уравнение цепи неодно родное. Поэтому переходный процесс можно рассматривать как наложе­ние у ста но вившегося и свободного процессов. Так, для напряжения на емкостном элементе

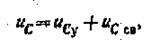
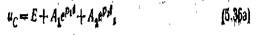
где составляющая свободного процесса совпадает с (5.30), а составляющая уста­новившегося процесса и_с = Е, т. е. общее решение для напряжения

а зарядный ток

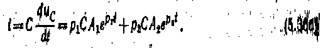
До замыкания ключа напряженения на емкостном элементе и тока в цепи не было. Поэтому в соответствии с законами ком­мутации получим для момента включения ключа (t= 0) два уравнения для опреде­ления двух постоянных А_{ и А_а:

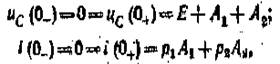
откуда

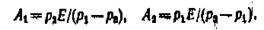
Ограничимся здесь анализом колеба- Рис. 5.10. тельного (5.31) процесса зарядки. Выпол-

нив преобразования, аналогичные переходу от (5.33) к (5.34), получим зависимости изменения во времени напряжения на емкостном элементе и зарядного тока (рис. 5.10,6):

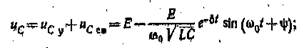
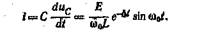
Напряжение на емкостном элементе достигает наибольшего значения в момент времени Оно тем больше, чем постоянная времени т = 1/6 больше периода собственных колебаний Т_й = 2л/и₀, и в пределе может превышать почти в 2 раза установившееся напряжение. Такое перенапряжение может быть опасно для изо­ляции высоковольтных установок. Чтобы исключить перенапряжение, нужно осу­ществить апериодический режим зарядки, например включить последовательно в цепь добавочный резистор.

Дата добавления: 2015-08-02