Прочность и удельное объемное сопротивление некоторых материалов

Наименование вещества	^ег	6„ ^мв/"*	су. Ом-и
Трансформаторное масло	2.1—2,4	15— '20	Ю14— (0и
Совол	4.8-5	Н— 18	К)»— 10»
Вазелин	2,2—2.6	'20—25	5- 10^1г— 10«
Полиэтилен	2,2—2,4	35—60	1 О*— ЮЧ
Лавсан	3,0— 3,5	80—120	10»—!0">
Полиаиядлхлоркд (плаетнкаты)	6—8	6—15	101»— Ю^и
Парафин	2.0—2,2	22—32	10»— Ю"
Эбонит	3,0—3,5	15—20	1012—Ю"
Гетинакс	6-8	20-^0	10»— 10"
Слюда (мусковит)	6,5—7,2	98—175	1012—ЮЧ
Мрамор	8—9	1,0—4,0	10'— 10»
Шифер	6-8	0,5—1,5	]0в-,10!
Аебестодемеет	6-8	2,0—3,0	100—103

* Электрическая прочность всех материалов указана для действующего значения переменного напряжения (си. 5 2.6).

Так как электрическое поле всегда существует между различными деталями электротехнических устройств, находящихся под напряже­нием, между этими деталями есть емкость. Конечно, в ряде случаев эта емкость настолько мала, что ее влиянием можно пренебречь.

Линейный емкостный элемент (рис. 2.3, в) является схемой заме­щения любой части электротехни­ческого устройства, если значение заряда пропорционально напряже­нию. Если же заряд не пропорцио­нален напряжению, то схемой заме­щения будет нелинейный емкостный элемент, который задается нелиней­ной кулон-вольтной характеристикой

q (u_c).

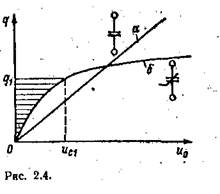
На рис. 2.4 приведены кулон-воль-тные характеристики линейного (а) и

нелинейного (б) емкостных элементов, а также условные обозначения таких элементов на схемах замещения.

Если напряжение, приложенное к емкостному элементу, будет изменяться (увеличиваться или уменьшаться), то будет изменяться и заряд, т. е. в емкостном элементе появится ток. Положительное на­правление тока в емкостном элементе выберем совпадающим с.поло­жительным направлением напряжения, приложенного к емкостному элементу. При этом ток

I_ab=i_c=dq/dt (2.10)

В линейном емкостном элементе с учетом (2.7) ток

I_c=Cdu_c/dt (2.11)

Если за время t₁напряжение на емкостном элементе изменится от нуля до u_c1то в электрическом поле элемента будет накоплена энергия

Или с учетом (2.10)

(2.12)

где q₁ — свободный заряд при напряжении u_с = u_с1 (рис. 2.4).

Как следует из (2.12), энергия, запасенная в электрическом поле емкостного элемента при напряжении u_с, пропорциональна соответ­ствующей площади, заключенной между кулон-вольтной характерис­тикой и осью ординат (рис. 2.4, где заштрихована площадь, пропор­циональная энергии электрического поля нелинейного емкостного элемента при напряжении ис,).

Из (2.12) с учетом (2.7) следует, что у линейного емкостного эле­мента при напряжении u_с энергия электрического поля

W_и=Cu²c/2=qu_c/2 (2.13)

Приведенный анализ показывает, что емкостные элементы электри­ческих цепей можно, как и индуктивные элементы, рассматривать в качестве аккумуляторов энергии, в которых может накапливаться энергия.

Таблица 2.2. Условные графические обозначения катушек индуктивности и конденсаторов

В табл. 2.2 приведены некоторые условные графические обозначе­ния катушек индуктивности и конденсаторов.

В дальнейшем при анализе линейных электрических цепей сину­соидального тока термин «линейный» дополнительно оговариваться не будет.

Дата добавления: 2015-08-02