Применение закона Ома и законов кирхгофа для расчетов электрических цепей

При помощи закона Ома и двух законов Кирхгофа можно рассчитать режим работы электрической цепи любой сложности.

Общей задачей расчета является определение токов во всех участ­ках цепи при заданных параметрах элементов цепи и известной кон­фигурации цепи.

Для составления уравнений по закону Ома и двум законам Кир­хгофа следует прежде всего выбрать (произвольно) положительные направления токов во всех ветвях рассчитываемой электрической цепи.

При записи уравнений для узлов цепи по первому закону Кирхгофа необходимо иметь в виду, что число независимых уравнений на единицу меньше общего числа узлов у, т. е. нужно составить у — 1 уравнений. Действительно, если составить уравнения для всех у узлов, то ток каждой ветви войдет дважды в уравнения для узлов, так кап ветвь соединяет два узла, причем с противоположными зна­ками (ток каждой ветви направлен к одному из узлов, и следователь­но, направлен от другого узла). При суммировании всех левых частей

уравнений составленных по первому закону Кирхгофа получается тождественно нуль.

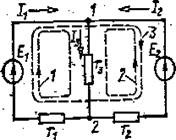
Рис. 1.11

При составлении уравнений на основании второго закона Кирхгофа необходимо также получить независимую систему. В частности, будет получена независимая система, если выбрать контуры так, чтобы каждый следующий содержал хотя бы одну ветвь, не вошед-

шую в контуры, для которых уже составлены уравнения. Такие контуры называются независимыми контурами, так как их уравнения взаимно независимы.

Число неизвестных токов равно числу ветвей в. Для определения этих токов необходимо составить в независимых уравнений. Так как по первому закону Кирхгофа составляется у — 1 независимых уравнений, то на основании второго закона Кирхгофа должно быть составлено в — (у — 1) уравнений.

Например, для цепи по рис. 1.11 можно было бы составить два уравнения на основании первого закона Кирхгофа для двух узлов (выбранные положительные направления токов показаны стрел­ками). Для узла 1:

I₁+I₂-I₃=0 (1.8)

для узла 2:

I₃-I₁-I₂=0 (1.9)

На основании второго закона Кирхгофа и закона Ома можно было бы составить три уравнения для трех контуров. Для контура 1:

r₁I₁+r₃I₃ =E₁ (1.10)

для контура 2:

r₂I₂+r₃I₃ =E₂ (1.11)

для контура 3;

r₁I₁+r₂I₂ =E₁- E₂ (1.12)

Но схема цепи по рис. 1.11 содержит только три ветви, т. е. для ее расчета необходимы три независимых уравнения.

Для этой схемы число узлов у = 2, т. е. по первому закону Кирх­гофа должно быть составлено только одно независимое уравнение: (1 8) или (1.9). Действительно, одно из этих уравнений получается из другого умножением на —I.

Из трех контуров на рис. 1.11 независимыми можно, например, считать 1-й и 2-й (во 2-й входит ветвь 2, которую не содержит, 1-й контур). Действительно, уравнение (1.16) можно получить, составив соответственно разности правых и левых частей уравнений (1.10 и (1.11). В качестве независимых для схемы цепи по рис. 1.40 можно взять и любую другую пару контуров.

После совместного решения системы независимых уравнений опре­деляются токи в ветвях цепи. Если для какого-либо тока будет полу­чено отрицательное значение, то из этого следует, что его действи­тельное направление противоположно выбранному положительному направлению.

Совместное решение системы уравнений, составленных на основа­нии двух законов Кирхгофа для сложной цепи, часто требует зна­чительной затраты времени. Поэтому желательно, когда это возможно, вести расчеты более простыми методами, которые рассматриваются в следующих параграфах. Все эти методы основываются на законах Ома и Кирхгофа.

Вряде случаев расчет сложной электрической цепи существенно упрощается, если в этой цепи заменить группу резистивиых элементов другой эквивалентной группой, в которой резистивные элементы соединены иначе, чем в заданной цепи. Взаимная эквивалентность двух групп резистивных элементов определяется тем, что после за­мены режим работы остальной части электрической цепи не изменится.

В общем случае цепь из резис­тивных элементов по схеме n-лучевая звезда может быть замещена эквивалентной цепью по схеме n -сторонний многоугольник. В обрат­ном направлении преобразование возможно в ограниченном числе случаев. В частности, преобразования в обоих направлениях возмож­ны для цепей резистивных элементов по схемам треугольник и трехлучевая звезда. Такое преобразование часто применяется для слож­ных цепей постоянного тока, но особенно важно при расчетах слож­ных цепей трехфазного тока (гл. 3).

Условия эквивалентности цепей по схемам треугольник и звезда (рис. 1.12) проще всего определяются приравниванием значений сопротивлений и проводимостей между одноименными узлами этих.

Чтобы определить сопротивление ветви по схеме звезда r_а найдем:

r_a=r_AB r_CAI ∑r ∆ (1.13)

Два другие выражения для определения сопротивлений ветвей цепи по схеме звезда получим путем простой циклической перестановки индексов:

r_B=r_BC r_ABI ∑r ∆ (1.14)

r_C=r_CA r_BCI ∑r ∆ (1.15)

Определим сопротив­ление ветви эквивалентной цени по схеме треугольник:

r_AB=r_A+ r_B + r_A r_B /r_C (1.16)

Посредством циклической перестановки индексов в (1.24) найдем вы­ражения для сопротивлений двух других ветвей

r_BC=r_B+ r_C + r_B r_C /r_A (1.17)

r_CA=r_C+ r_A + r_C r_A /r_B (1.18)

Дата добавления: 2015-08-02