Различные представления синусоидальных величин

Известно несколько способов представления величин, изменяющих­ся по синусоидальному закону: в виде тригонометрических функций, в виде графиков изменений функций во времени, в виде вращающихся векторов и, наконец, в виде комплексных чисел.

В § 2.4 и 2.5уже применялись представления синусоидально изме­няющихся величин в виде тригонометрических функций, например (2.14), (2.15), и в виде графика изменений функций во времени (рис. 2.6).

Теперь рассмотрим представление величин, изменяющихся по синусоидальному закону, в виде вращающихся векторов и комплекс­ных чисел.

Представление синусоидальных величин вращающимися век­торами. Для представления синусоидально изменяющейся величины

a=A_msin(wt+¥)

с начальной фазой ¥ вращающимся вектором построим (рис. 2.10, а) радиус-вектор А_m этой величины длиной (в масштабе построения), равной амплитуде А_m, и под углом т|) к горизонтальной оси. Это будет его исходное положение в момент начала отсчета времени t = 0. Из конца радиуса-вектора А_m, находящегося в начальном положении, опустим на горизонтальную ось перпендикуляр, длина которого равна А_msin¥. Предположим, что радиус-вектор вращается с постоянной угловой частотой w = 2п/Т = 2пf против направления движения часовой стрелки, где Т — период, f— частота вращения.

В момент времени t₁ радиус-вектор A_m будет повернут относительно начального положения на угол wt₁ длина перпендикуляра, опущен­ного из его конца, будет равна A_msin(wt₁+¥).

Очевидно, длина перпендикуляра, опущенного из конца вращаю­щегося радиуса-вектора на горизонтальную ось, будет максимальной в момент временя t₂, при котором wt₂+¥=п/2

A_msin(wt₂+¥).= A_msin (п/2) = A_m

Рядом с окружностью, описываемой концом вращающегося радиуса-вектора, можно построить в прямоугольной системе координат график зависимости синусоидальной величины A_msin(wt+¥) от фазы wt или от времени ((рис. 2.10, б). В момент t₂ синусоидальная величина а достигает максимального значения. Далее по мере вращения радиуса-вектора синусоидальная величина a=A_msin(wt+¥), оставаясь положительной, уменьшается, достигая нулевого значения в момент времени t₄ a в следующие моменты времени, например t₅ и t₆ мгновен­ные значения синусоидальной величины а получаютсяотрицательными, с момента /₇ снова положительными и т. д.

Применение вращающихся векторов позволяет компактно предста­вить на одном рисунке совокупность различных синусоидально изме­няющихся величин одинаковой частоты при анализе сложной электри­ческой цепи.

Представление синусоидальных величин комплексными числами. От представления синусоидальных величин вращающимися ра­диусами-векторами нетрудно перейти к представлению синусоидальных величин комплексными числами.

Дня того чтобы представить заданную в тригонометрической форме синусоидальную величину

а= A_msin(wt+¥) (2.20)

с начальной фазой ¥ комплексным числом, проведем на комплексной. плоскости (рис. 2.11) из начала координат под углом ф к оси действи­тельных величин и чисел вектор, длина которого в масштабе построе­ния равна амплитуде А_т синусоидальной величины. Конец этого век­тора находится в точке, которой соответствует определенное комплекс­ное число — комплексная амплитуда синусоидальной величины:

A_m= A_meⁱ¥= A_m <¥

Так же обозначается и соответствующий комплексной амплитуде вектор на комплек­сной плоскости

При увеличении во времени фазы wt+¥ синусоидальной величины угол между век-

тором и осью действительных величин растет, т. е. получается вращающийся вектор

A_meⁱ¥ ^(wt+¥) = A_mcos(wt+¥)+i A_msin(wt+¥)

Нетрудно видеть, что мнимая часть вращающегося вектора равна за­данной синусоидальной величине (2.20).

По существу представление синусоидальной величины комплексной амплитудой Л_т и соответствующим ей вектором на комплексной плос­кости геометрически подобно представлению той же синусоидальной величины вращающимся радиусом-вектором А_m в момент времени t = 0 (рис. 2.10, а). Поэтому может создаться впечатление, что оба представления синусоидальных величин практически совпадают. В дей­ствительности это не так. В случае представления синусоидальных величин комплексными числами можно применить весьма эффективный комплексный метод анализа электрических цепей синусоидального тока, который в настоящее время завоевал всеобщее признание.

Вектор на комплексной плоскости, длина которого в масштабе построения равна действующему значению синусоидальной величины, и соответствующее комплексное число называются комплексным дей­ствующим значением синусоидальной величины:

(2.21)

Так же обозначается и сам вектор на комплексной (рис. 2.11).

Применяются три формы записи комплексного значения синусои­дальной величины:

показательная форма

тригонометрическая форма

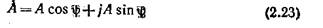
и алгебраическая форма

где А' = Acos¥ и А’’= Asin¥ —действительная и мнимая состав­ляющие комплексного значения синусоидальной величины;

Переход от показательной формы к тригонометрической выполня­ется при помощи формулы Эйлера:

При значениях угла ¥ = п/2 и ¥= —п/2 из формулы Эйлера следуют два часто встречающихся соотношения:

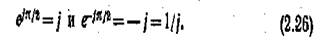
При анализе цепей синусоидального тока применяют главным образом комплексные действующие значения синусоидальных вели­чин; сокращенно их называют комплексными значениями синусоидаль­ных величин, а соответствующие векторы на комплексной плоскости — векторами комплексных значений. Например, синусоидальному току.

соответствует комплексное значение тока

Совокупность векторов комплексных значений синусоидальных величин одной частоты называется векторной диаграммой. Пользуясь векторной диаграммой, сложение и вычитание комплексных значений можно заменить сложением и вычитанием соответствующих векторов комплексных значений. Это иногда упрощает расчеты и делает их наглядными-

Взаимное расположение векторов комплексных значений на вектор­ной диаграмме не изменится, если начальные фазы ¥ всех комплексных значений уменьшить (увеличить) на одну и ту же величину. Это озна­чает лишь одновременный поворот всех векторов на один и тот же угол. Часто при анализе электрических цепей векторную диаграмму строят так, чтобы вектор одного комплексного значения был направлен вдоль оси действительных величин. Такой вектор комплексного значения назовем исходным вектором.

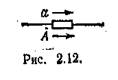
Направления синусоидальных величин (ток, напряжение и др.), определяющих режим электрической цепи, периодически изменяются, но одно из двух направлений принимается положительным. Это направление выбирается произвольно и показывается стрелкой на схеме соответствующего участка электрической цепи.

При выбранном поло-жительном направлении синусоидальная величина представляется мгновенным значением а = A_msin(wt+¥) и соответствующим комплексным значением А = А<¥ (2.21). Следовательно, взаимно однозначному представлению синусоидальных токов, напряжений и других величин в виде мгновенных и комплексных значений соответствуют их одинаковые положительные направления (рис. 2.12),

Дата добавления: 2015-08-02