Закон Ома в комплексной форме для резистивного, индуктивного и емкостного элементов

Зависимости между токами и напряжениями резистивных, индук­тивных и емкостных элементов определяются происходящими в них физическими процессами. Математическое описание физических явле­ний для каждого из этих элементов зависит от выбранного способа аналитического представления синусоидальных величин. В дальней­шем при аналитическом представлении синусоидальных токов, напря­жений и т. д. будем пользоваться как тригонометрическими функциями и для наглядности их графиками, так и комплексными значениями, для которых разработан эффективный математический аппарат анализа электрических цепей.

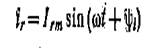
А. Резистивный элемент. Выберем положительное направление синусоидального тока

в резистивном элементе с постоянным сопротивлением г совпадающим с положительным направлением синусоидального напряжения, при­ложенного к элементу (рис. 2.13). В этом случае для мгновенных значений напряжения-и тока справедливо соотношение, определяемое аналогично (1.1) законом Ома:

или

где амплитуды тока и напряжения связаны соотношением

U_rm=rI_rm (2.27а) а их начальные фазы одинаковые:

¥_u= ¥_i (2.276)

т. е. ток и напряжение в резистивном элементе изменяются синфазно — совпадают по фазе, как показано на рис. 2.13 для начальной фазы ¥_u= ¥_i > 0.

Разделив правую и левую части выражения (2.27а) на Ã, получим соотношение для действующих значений напряжения и тока резистивного элемента

U_r=rI_r (2.28)

Представим теперь синусоидальные ток и напряжение резистивного элемента соответствующими комплексными значениями (2.22):

I_r=I_reⁱ¥_I и U_r=U_r eⁱ¥_u

Так как U_r,=rIr (2.28) и ¥_u = ¥₁(2.276), то для комплексных значений тока I_r, и напряжения U_г резистивного элемента получим закон Ома в комплексной форме:

U_г = rIr (2.29)

Соотношение между комплексными значениями тока и напряжения для резистивного элемента наглядно иллюстрируется векторной диаграммой элемента (рис. 2.14). Из векторной диаграммы также видно, что векторы комплексных значений тока и напряжения рези­стивного элемента совпадают по фазе.

Б. Индуктивный элемент. Если в индуктивном элементе ток синусоидальный:

то по закону электромагнитной индукции (2.3) на индуктивном элементе появится напряжение

где амплитуды напряжения и тока связаны соотношением

а их начальные фазы — соотношением

Разделив правую и левую части выражения (2.30а) на Ã, получим соотношение для действующих значений напряжения и тока индуктив­ного элемента:

На рис. 2.15 показан график мгновенных значений синусоидальных тока и напряжения индуктивного элемента (построен при ¥_i > 0),

из которого видно, что синусоидальный ток отстает по фазе от синусоидального напряжения

Индуктивное сопротивление пропорционально угловой частоте синусоидального тока, при постоянном токе (w = 0) оно равно нулю. По этой причине многие аппараты и машины, предназначенные для работы в цепи переменного (синусоидального) тока, нельзя включать в цепь постоянного тока. Для постоянного тока их сопротивление относительно мало, и большой постоянный ток может быть для них разрушительным (например, для первичной обмотки трансформатора в радиоприемнике).

Представим синусоидальные ток i_l и напряжение u_l индуктивного элемента соответствующими комплексными значениями:

На рис. 2.16 приведена векторная диаграмма для индуктивного элемента. На векторной диаграмме показано, что вектор комплексного значения тока /, отстает по фазе от вектора комплексного значения напряжения U_Lна угол п/2, что соответствует сдвигу фаз ф = я/2 на рис. 2.15. Пользуясь выражениями (2.31) и (2.26), получим закон Ома в комплексной форме для индуктивного элемента;

Входящая в это выражение величина iwL=ix_L называется комп­лексным сопротивлением индуктивного элемента, а обратная ей вели­чина I/iwL =-ib_L — комплексной проводимостью индуктивного эле­мента.

Комплексное значение напряжения на индуктивном элементе можно выразить и через комплексное значение потокосцепления.

Из (2.1) следует, что ¥ = Li_L, и по (2.32)

U_L=-E_L=iw¥ (2.33)

Это — математическая формулировка закона электромагнитной ин­дукции (2.3) в комплексной форме.

В. Емкостный элемент. Если напряжение между выводами ем­костного элемента изменяется по синусоидальному закону:

u_c=U_cmsin(wt+¥_u)

то по (2.11) синусоидальный ток

i_c=Cdu_c/dt=wCU_cmcos(wt+¥_u)=I_cmsin(wt+¥_u+п/2)= I_cmsin(wt+¥_u)

где амплитуды связаны соотношением

I_cm=Wcu_CM (2.34a)

а начальные фазы соотношением

¥_i=¥_u+ п/2 (2.34б)

Разделив правую и левые части выражения (2.34а) на Ã, получим соотношение для действующих значений напряжения и тока емкост­ного элемента:

Величина b_с=wС в выражении (2.35), единица которой Ом^-1 = См, называется емкостной проводимостью, а обратная величина х_с = I /wС— емкостным сопротивлением. Значения величин х_с и b_с являются пара­метрами емкостных элементов цепей синусоидального тока.

В противоположность индуктивному сопротивлению емкостное сопротивление уменьшается с увеличением частоты синусоидального тока. При постоянном напряжении емкостное сопротивление бесконечно велико.

На рис. 2.17 показан график мгновенных значений синусоидальных напряжения и тока для емкостного элемента (построен при ¥_u > 0), из которого видно, что синусоидальное напряжение u_сотстает по фазе от синусоидального тока i_с на угол ¥_u-¥_n = п /2, т. е. сдвиг по фазе между напряжением и током ¥ = ¥_u-¥_i=- п /2.

Представим синусоидальные ток i_с и напряжение u_с емкостного элемента соответствующими комплексными значениями:

i_с=i_с^еi1 и u_с=u_с ^еi1

На рис. 2.18 приведена векторная диаграмма для емкостного элемента. На векторной диаграмме показано, что вектор комплексного значения напряжения u_с отстает по фазе от вектора комплексного значения тока i_c на угол п /2.

Учитывая (2.34) и (2.26), получим закон Ома в комплексной форме для емкостного элемента:

Величина 1/iwС =-ix_с, входящая в это выражение, называется комплексным сопротивлением емкостного элемента, а обратная ей величина iwС = iЬ_С — комплексной проводимостью емкостного эле­мента.

Дата добавления: 2015-08-02