Электрическая цепь с параллельным соединением ветвей

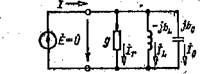
На рис. 2.33 представлена схема электрической цепи, состоящей из параллельного соединения резистивного, индуктивного и емкостного элементов. Будем считать заданными проводимость резистивного элемента комплексные проводимости ипдуктив и емкостного И элементов и одинаковое напряжение на каждом из элементов

о первому закону Кирхгофа определим комплексное значение общего тока, равного току источника ЭДС:

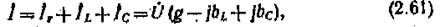
где учтено, что по [закону Ома I_г = qU; I_ь =-jb_lU комплексы токов в резистивиом, индуктивном и емкостном элементах. Сумма комплексных проводимостей всех параллельных ветвей в выражении (2.61) равна комплексной проводимости данной цепи (в алгебраической форме):

Обратная величина комплексной проводимости 1/Y = Z = Rе-это комплексное сопротивление. Поэтому в показательной форме комплексная проводимость

и в тригонометрической форме

где

цепи или 'полная проводимостьцепи;

На комплексной плоскости (рис. 2.34) слагаемые комплексной про-,_Мост1 цепи изображены в виде векторов для двух случаев: Ь, >• Ь_с (рис2 34 а) Ь, >• Ь (рис. 2.34, б). В первом случае комплексная проводимость цепи индуктивный характер, во втором емкостный.

Подставив значение комплексной проводимости цепи в показа­тельной форме (2.63а) в (2.61), получим комплексное значение тока в виде

Из (2.64) следует, что действующее значение тока в неразветвленной части цепи

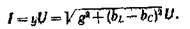
На рис. 2.35 приведены векторные диаграммы напряжения и токов рассматриваемой цепи дли двух случаев: Ь,. > Ь_с (рис. 2.35, и) и. (рис. 2.35, 6) при одинаковом напряжении 0. Если комплексная проводимость цепи имеет индуктивный характер, то общий ток (в неразветвленной части цепи) отстает по фазе от напря­жения, так как гр;. Если комплексная проводимость цепи имеет емкостный характер, то общий ток опережает по фазе на­пряжение, так как Заметим, что, как и ранее, положительные значения угла ф отсчитываются против направления Движения стрелки часов от вектора комплексного значения тока I. Комплексная мощность анализируемой цепи

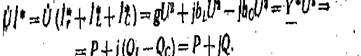
|Если электрическая цепь содержит несколько резистивных, индуктивных и емкостных элементов, включенных параллельно, то комплекс-

ЭДС Е источника, а тока в индуктивном элементе не было. Поэтому

Откуда

Подставим эти значения в (5.32а) а учтем, что по формуле Эйлера (2.25}

В результате получим зависимость изменения напряжения на емкостном эле­менте от времени в виде

Сумму косинусоидальной и синусоидальной функций можно заменить одной синусоидальной функцией. Для этого положим, что отношение w₀/ б =tqф т.е.- будем считать, что wи б — катеты прямоугольного треугольника (рис. 5.7), гипо­тенуза которого

Разделив и умножив (5.33) на 1/LC, получим:

и по (5.27) разрядный ток

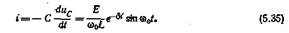
Зависимости (5.34) и (5.35) показывают, что напряжение емкостного элемента И разрядный ток можно рассматривать как синусоидально изменяющиеся во вре­мени величины, но с амплитудами, умень­шающимися по экспоненциальному закону при постоянной времени т= 1/6= 21./г.

Для построения соответствующих за­висимостей можно сначала построить вспомогателыне экспоненты

Рис. 5.7.

Кривые изменения напряжения и тока (рис. 5.И) должны вписаться в пределы, ограниченные указанными вспомогательными экспонентами. Для нахождения ха­рактерных точек кривой изменения напряжения на емкостном элементе, таких как и_с (0) = Е и «_с (0 = 0, на рисунке показана точками вспомогательная кривая —

синусоида.

Рассмотрим теперь случай действительных отрицательных корней р_1Л характе­ристического уравнения (5.29).

Если г²/ 4L² > 1/LС, то действительные корни имеют различные значения, причем р₂ < р₁< 0. Для нахождения А₁ к А₂ в общем решении (5.30) восполь­зуемся аналогично предыдущему законами коммутации для емкостного и индук­тивного элементов:

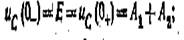
Подставив найденные значения постоянных интегрирования в (5.30), получим

зависимости напряжения на ёмкостном эле­менте:

тока разрядки:

Кривые изменения напряжения и тока "по-

казаны на рис. 5.9, где пунктиром нанесены также вспомогательные экспоненты. В течение всего переходного процесса напряжение и ток не изменяют знака, т. е. разрядка емкостного элемента апериодическая.

Для предельного случая апериодического процесса, если г²/ 4L²=1/LС, ха­рактеристическое уравнение имеет два одинаковых действительных корня р1=р₂=р= —г/2L (кратные корни). При кратных корнях общее решение диффе­ренциального уравнения (5.28) отличается от (5.30) и имеет вид:

где постоянные А₁ и А₂определяются на основании законов коммутации. Зависи­мости напряжения на емкостном элементе и тока для предельного апериодического процесса разрядки

Дата добавления: 2015-08-02