Неразветвленная цель синусоидального тока

В неразветвленной цепи (рис. 2.24) при действии источника сину­соидальной ЭДС

ток также синусоидален:

и напряжения на резистивном, индуктивном и емкостном элементах:

Для расчета режима неразветвленной цепи синусоидального тока применим комплексный метод. Представим все синусоидальные вели­чины соответствующими комплексными значениями по (2.21):

На рис. 2.24 стрелками изображены положительные направления тока, ЭДС и напряжений.

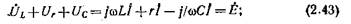
Выберем направление обхода контура по направлению движе­ния часовой стрелки и запишем уравнение по второму закону Кирхгофа (2.41):

здесь учтен закон Ома для резистивного (2.29), индуктивного (2.32) и емкостного (2.36) элементов.

Из (2.43). найдем комплексный ток в цепи:

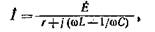
напряжение между выводами неразвет­вленной цепи (рис. 2.24).

Величина, стоящая в знаменателе выражения для комплексного тока (2.44), называется комплексным сопротивлением(неразветвленной цепи):

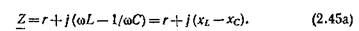
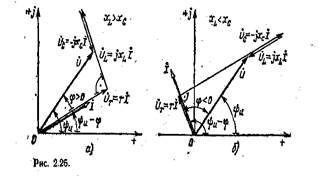
Каждому значению комплексного сопротивления 2, т. е. комплекс­ному числу, соответствует точка на комплексной плоскости. Ее поло­жение однозначно определяется вектором на комплексной плоскости (рис. 2.25). Этот вектор является геометрической интерпретацией комплексного сопротивления и имеет такое же обозначение 7,.

Слагаемые комплексного сопротивления изображены на рис. 2.25 также в виде векторов для двух случаев: х_Lxс (рис. 2.25,о) и х_Lxс (рис. 2.25, б). В первом случае комплексное сопротивление имеет индуктивный характер, во втором — емкостный. Геометрическая ин­терпретация комплексного сопротивления позволяет легко перейти от алгебраической формы записи комплексного сопротивления (2.45 а) к тригонометрической и показательной формам:

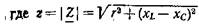
модуль комплексного сопротивления или полное сопротивление, ф = агс1§ -^ - ^ — аргумент комплекс-

ного сопротивления. В зависимости от знака величины аргумент комплексного сопротивления может быть либо положитель­ным (индуктивный характер), либо отрицательным (емкостный характер),

Подставим значение комплексного сопротивления в показательной форме (2.45в) в (2.44). При этом ток в цепи будет определен по закону Ома для неразветвленнойцепи:

Если значения параметров резистивного, индуктивного и емкост­ного элементов известны и задано напряжение между выводами нераз­ветвленной цепи (рис. 2.24), то по закону Ома для неразветвленной цепи (2.46) однозначно определяется комплексный ток в цепи. При известном комплексном токе в цени комплексные напряжения на ре-зистивном, индуктивном и емкостном элементах рассчитываются соот­ветственно по (2.29), (2.32), (2.36).

На рис. 2.26 приведены векторные диаграммы тока и напряжений неразветвленной цепи (рис. 2.24) для двух случаев: (рис. 2.26, а) (рис. 2.26, б) при одинаковом заданном напря­жении. Если комплексное сопротивление цепи имеет индуктивный характер, то ток / отстает по фазе от напряжения U, так как ф > 0 (рис. 2.25, а) к по (2.47) ¥_i <¥_u. Если комплексное сопротивление цепи имеет ем­костный характер, то ток в цепи опережает но фазе напряжение, та к как Ф<0 (рис. 2.25, 6) и по (2.47) ¥_i <¥_u. На векторной диаграмме положительное значение угла ф отсчитывается против направления движения часовой стрелки от вектора комплексного значения тока /, а отрицательное значение — по направлению движения часовой стрелки.

При нескольких последовательно соединенных резистивных индук­тивных и емкостных элементах комплексное сопротивление

где Я — активное сопротивление и реак­тивное сопротивление этой неразветвленной цепи. В активном соп­ротивлении происходит необратимое преобразование электрической энергии в другие виды энергии, а в реактивном сопротивлении не про­исходит.

Введенные здесь понятия об активном и реактивном сопротивлениях неразветвленной цени применяются и для характеристики более сложных цепей. В общем случае можно говорить об активном и реак­тивном сопротивлениях любой пассивной цепи синусоидального тока, имеющей два вывода.

Напряжение на элементах схемы замещения, соответствующих активному или реактивному сопротивлению цепи, называется падением напряжения.

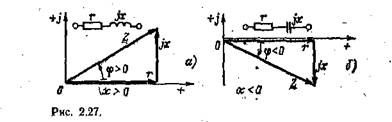
Выражению (2.48) соответствуют треугольники сопротивлений на комплексной плоскости (рис. 2.27). На рис. 2.27, а построен тре­угольник сопротивлений при х > 0, т. е. при индуктивном характере комплексного сопротивления, а на рис. 2.27, б — при х <0, т. е. при емкостном характере комплексного сопротивления. Там же показаны схемы замещения соответствующих электрических цепей. Из треуголь­ников сопротивлений наглядно определяются тригонометрическая и показательная формы комплексного сопротивления неразветвленной пассивной цепи, совпадающие с выражениями (2.45), причем полное сопротивление г и аргумент ф комплексного сопротивления (2.48) будут:

Дата добавления: 2015-08-02