Неразветвленная магнитная цепь

Задачей расчета неразветвленной магнитной цепи в большинстве случаев является определение МДС Р = /да, необходимой для того, чтобы получить заданные значе­ния магнитного потока или маг­нитной индукции в некотором участке магнитопровода (чаще всего в воздушном зазоре).

На рис. 6.9 приведен пример не разветвленной магнитной це­пи — магнитопровод постоянно­го поперечного сечения 5! с за­зором. На этом же рисунке ука­заны другие геометрические раз­меры обоих участков магнито­провода: средняя длина маг- Рис. С.9. ннтной линии первого участка из ферромагнитного материала и длина /₂ второго участка — воздуш­ного зазора. Магнитные свойства ферромагнитного материала заданы основной кривой намагничивания В (Я) (рис. 6.10) и тем самым по (6.4) зависимостью \\_а (Я).

По закону полного тока (6.2)

где Н₁ и Н ₂ — напряженности магнитного поля в первом и втором участках.

В воздушном зазоре значения магнитной индукции В_й и напря­женности Я₂ связаны простым соотношением В_г = |1₀Я₂, а для участка из ферромагнитного материала В₁ = ^₀1^1- Кроме того, в неразвет­вленной магнитной цепи магнитный поток одинаков в любом поперечном сечении магнптопровода:

где S_1и S₂ — площади поперечного сечения участка из феррома­гнитного материала и воздушного зазора.

Если задан магнитный поток Ф, то по (6.6) найдем значения индук­ций В_г и В₂. Напряженность поля Н₁ определим по основной кривой намагничивания (рис. 6.10), а Н_а = В₂х._а. Далее по (6.5) вычислим необходимое значение МДС.

Сложнее обратная задача: расчет магнитного потока при задан­ной МДС Р.

Заменив в (6.5) напряженности магнитного поля значениями ин­дукции, получим:

или с учетом (6.6)

магнитное сопротивление участка магнит­ной цепи, причем магнитное сопротивление й-го участка нелинейное, если зависимость В (//) для этого участка нелинейная (рис. 6.10), т.

Для нелинейного магнитного сопротивле­ния г„ можно построить вебер-амперную ха­рактеристику — зависимость магнитного по­тока Ф от магнитного напряжения V '«на со­ответствующем участке магнитопровода. Веберамперная характеристика участка маг­нитопровода рассчитывается по основной кривой намагничивания ферромагнитного материала В (Я). Чтобы по­строить вебер-амперную характеристику, нужно ординаты и абсциссы всех точек основной кривой намагничивания умножить соответственно на площадь поперечного сечения участка 5 и его среднюю длину /,

На рис. 6.11 приведены вебер-амперные характеристики Ф СЛл) для нелинейного магнитного сопротивления г_л (ферромагнитного участка) и Ф ((/_м2) для линейного магнитного сопротивления (воздушного зазора) магнитопровода по рис. 6.9.

Между расчетами нелинейных электрических цепей постоянного тока и магнитных цепей с постоянными МДС нетрудно установить аналогию. Действительно, из уравнения (6.7) следует, что магнитное напряжение на участке магнитной цепи равно произоедению магнит­ного сопротивления участка на магнитный поток. Эта за­висимость аналогична закону Ома для резистивного элемента электрической цепи постоянного тока u = г/(1.1).Сумма магнитных напря­жений в контуре магнитной цепи равна сумме МДС этого контура, что аналогично второму закону Кирхгофа для элек­трических цепей постоянного тока %и = 2Я (1.8).

Продолжая дальше аналогию между электрическими цепями постоянного то­ка и магнитными цепями с постоянными МДС, представим неразветвленную маг­нитную цепь (рис. 6.9) схемой замеще­ния (рис. 6.12, а). Эта схема замещения и схема замещения нелинейной электри­ческой цепи с последовательным соеди­нением элементов (см. рис. 1.31) полно­стью аналогичны (с точностью до обоз­начения параметров элементов). Следовательно, для анализа не-разветвленных магнитных цепей (а также и разветвленных магнит­ных цепей) с постоянной МДС можно пользоваться всеми графиче­скими и аналитическими методами расчета нелинейных электриче­ских цепей постоянного тока (см. § 1.21).

В качестве иллюстрации ограничимся применением для анализа неразветвленной магнитной цепи рис. 6Л2, а графических методов:

метода сложения вебер-амперных характеристик (рис. 6.11) и метода нагрузочной ха­рактеристики (рис. 6.12,6). Согласно первому методу построим вебер-амперную ха­рактеристику всей неразветв­ленной магнитной цепи графически складывая по напряжению вебер-амперные характери­стики ее двух участков. При

известной МДС Р = /да по вебер-амперной характеристике всей маг­нитной цепи определим магнитный поток Ф, а по вебер-амперным характеристикам участков магнитопровода — магнитные напряжения на каждом из них.

Согласно второму методу для второго (линейного) участка построим нагрузочную характеристику (1.39).

т. е. прямую, проходящую через точку Р на оси абсцисс и точку на оси ординат. Точка пересечения нагрузочной характеристики с вебер-амперной характеристикой ферромагнитного участка цепи Ф (^ш) определяет магнитный поток Ф в цепи и магнитные напряже­ния на ферромагнитном участке И_к1 и воздушном зазоре (У_м2. Значе­ние индукции в воздушном зазоре В_а = Ф/S₄.

6.5. НЕРАЗВЕТВЛЁННАЯ МАГНИТНАЯ ЦЕПЬ С ПОСТОЯННЫМ МАГНИТОМ

Рассмотрим расчет простейшей неразветвленной магнитной цепи с постоянным магнитом. Предположим, что тороид длиной I и пло­щадью поперечного сечения 5 (рис. 6.13, а) изготовлен из магнитно-твердого материала, часть предельного статического цикла гистере­зиса которого В (Я) изображена на рис. 6.13, 6, Материал торолда был предварительно намагничен так, что его магнитное состояние ха­рактеризуется остаточной индукцией В_г.

Вырежем из тороида участок длиной (рис. 6.13, в). Остав­шаяся часть тороида будет-постоянным магнитом, а в образовавшемся воздушном зазоре магнитное поле возбуждается этим постоянным магнитом. Пренебрегая неоднородностью магнитного поля в воздуш-

ном зазоре, будем считать, что всюду в зазоре магнитное поле харак­теризуется напряженностью магнитного поля Я„ и индукцией Учтем, что вследствие «выпучивания» магнитных линий в воз­душном зазоре площадь поперечного сечения воздушного зазора 5_В больше площади поперечного сечения постоянного магнита.

По закону полного тока (6.5) для контура, совпадающего со средней линией магнитопровода,

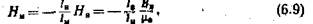
где Н„ и 1_Я — напряженность магнитного поля и длина средней линии постоянного магнита.

Из (6.8) следует, что

Кроме того, так как магнитный поток Ф в неразветвленной маг­нитной цепи постоянен, то

Подставив значение индукции в воздушном зазоре В_в из (6.10) в (6.9), получим уравнение прямой линии, проходящей через начало координат (рис. 6.13,6):

где— коэффициент размагничивания постоянного магнита.

Точка пересечения прямой „ и предельного статиче­ского цикла гистерезиса материала В (Н) определяет индукцию в маг­ните В = В_н, а следовательно, и индукцию в воздушном зазоре (6.10).

Если в воздушный зазор медленно вводить ферромагнитный за­мыкатель с малым магнитным сопротивлением, то значение индукции в магнитопроводе будет увеличиваться по частному гистерезисному циклу, показанному на рис. 6.13,6 пунктиром. При многократном магнитном замыкании и размыкании воздушного зазора изменение индукции магнита происходит по некоторому установившемуся част­ному циклу.

Для получения больших значений индукции в воздушном зазоре необходимо изготавливать постоянный магнит из магнитно-твердых материалов, т. е. с большим значением коэрцитивной силы Я_с.

Дата добавления: 2015-08-02