Свойства ферромагнитных материалов

Магнитное состояние любой точки изотропной среды, т. е. сред с одинаковыми свойствами во всех направлениях, вполне определяете вектором напряженности магнитного поля Н и вектором магнитного. индукции В, которые совпадают друг с другом по направлению.

Основная единица измерения магнитной индукции в системе С называется тесла (Тл); 1. Это нндукщ: такого однородного магнитного поля, в котором магнитный поток ' (см. § 2.3) через поверхность площадью 1 м², перпендикулярна направлению магнитных линий поля, равен одному веберу (Вб),

В вакууме индукция и напряженность магнитного поля связан простым соотношением: В магнип ноя постоянная. Для ферромагнитных материалов зависимость от напряженности магнитного поля В (Н) в общем случае.

Для того чтобы экспериментально исследовать магнитные ферромагнитного материала, необходимо все измерения прои. водить на образце, в котором магнитное поле однородное. Таким «разцом может быть тороид, изготовленный из исследуемого –феррома ннтного материала (рис. 6.5), длина магнитных линий в котором много больше его поперечных размеров (тонкостенный тороид). На тороиде находится равномерно навитая обмотка с числом витков.

Можно считать, что в тороиде из ферромагнитного изотропного материала с плотно намотанными витками все магнитные линии — окружности, а векторы напряженности и индукции магнитного поля

направлены по касательной к со­ответствующей окружности. Так, на рис. 6.5 показана средняя маг­нитная линия и векторы Н и В в одной из ее точек.

При расчете напряженности и индукции магнитного поля в тон­костенном тороиде можно считать, что все магнитные линии имеют одинаковую длину, равную длине средней линии 2лг.

Предположим, что ферромаг­нитный материал тонкостенного тороида полностью размагничен и

Рис. 6.5.

тока / в обмотке пет (В = 0 и Н = 0). Если теперь плавно увеличи­вать постоянный ток / в обмотке катушки, то в ферромагнитном ма­териале возникнет магнитное поле, напряженность которого опре­деляется законом полного тока (6.1):

(6.3>

Каждому значению напряженности Н магнитного поля в тонко­стенном тороиде соответствует определенная намагниченность ферро­магнитного материала, а следовательно, И соответствующее значение

магнитной индукции В.

Если начальное магнитное состояние материала тонкостенного то­роида характеризуется значениями Н = О, В = 0, то при плавном нарастании тока получим нелинейную зависимость. В (Я), которая называется кривой первоначального намагничивания (рис. 6.5, штрихо­вая линия). Начиная с некоторых значений напряженности Я маг­нитного поля индукция В в тонкостенном ферромагнитном тороиде практически перестает увеличиваться и остается равной В_таж. Зга область зависимости В (Я) называется областью технического насыщения.

Если, достигнув насыщения, начать плавно уменьшать постоянный ток в обмотке, т. е. уменьшать напряженность поля (6.3), то индукция также начнет уменьшаться. Однако зависимость В (И) уже не совпадет с кривой первоначального намагничивания. Изменив направление тока в обмотке и увеличивая его значение, получим новый участок зависимости 6 (Я). При значительных отрицательных значениях напряженности магнитного поля снова наступит техническое насыще­ние ферромагнитного материала. Если теперь продолжить экспери­мент: сначала уменьшать ток обратного направления, затем увеличи­вать ток прямого направления до насыщения и т. д., то после несколь-

ких циклов перемагничивания для зависимости В (Н) будет получена симметричная кривая (рис. 6.5, сплошная линия). Этот замкнутый цикл В (Я) называется предельной статической петлей гистерезиса (или предельным статическим циклом гистерезиса) ферромагнитного материала. Если во время симметричного перемагничивания область технического насыщения не достигается, то симметричная кривая В (Я) называется симметричной частной петлей гистерезиса ферромагнит­ного материала.

Предельный статический цикл гистерезиса ферромагнитных ма­териалов характеризуется следующими параметрами (рис. 6.5): Я_с -коэрцитивной силой. В_Г—остаточной индукцией коэффициентом прямоугольности.

По значению параметра Я_с предельного статического цикла гисте­резиса ферромагнитные материалы делятся на группы:

1) магнитные материалы с малыми значениями коэрцитивной силы Я_с<0,05 -т- 0,01 А/м называются магнитно-мягкими;

2) магнитные материалы с большими значениями коэрцитивной силы Я_с > 20 -т- 30 кА/м называются магнитно-твердыми.

Магнитно-твердые материалы используются для изготовления по­стоянных магнитов, а магнитно-мягкие — при изготовлении магни­тол р оводов электротехниче­ских устройств, работающих в режиме перемагничивания по предельному или частным циклам.

Магнитно-мягкие материа­лы в свою очередь делятся на три типа: магнитные материа­лы с прямоугольной предель­ной статической петлей гисте­резиса, у которых коэффициент прямоугольности йгг] > 0,95 (рис. 6.6, с);

магнитные материалы с округлой предельной статической петлей гистерезиса, у которых коэффициент прямоугольности 0,4 < </г^<;0,7 (рис. 6.6, б); магнитные материалы с линейными свойст­вами, у которых зависимость В (Я) линейная: В = \л.^„Н (рис. 6.6, в), где \1_Г — относительная магнитная проницаемость.

Все типы магнитных характеристик ферромагнитных материалов могут быть получены на образцах, изготовленных либо из различных ферромагнитных сплавов, либо из ферромагнитной керамики (фер­риты). Ценное свойство ферритов в отличие от ферромагнитных сплавов — их высокое удельное электрическое сопротивление.

Магнитопроводы из ферромагнитных материалов с прямоугольным предельным статическим циклом гистерезиса применяются в опера­тивной памяти цифровых электронных вычислительных машин, маг­нитных усилителях и других устройствах автоматики. Ферромагнит­ные материалы с округлым предельным статическим циклом гистере­зиса используются при изготовлении магнитопроводов электрических машин и аппаратов. агнитопроводы этих устройств обычно работают

в режиме перемагпичнваипя по симметричным частным циклам. При расчете магнитопроюдов таких электротехнических устройств сим­метричные частные циклы заменяют основной кривой намагничивания ферромагнитного материала, которая представляет собой геометриче­ское место вершин симметричных частных циклов тонкостенного фер­ромагнитного тороида (рис. 6.7), полученных при синусоидальном токе низкой частоты в обмотке.

По основной кривой намагничивания фер­ромагнитного материала определяют зависи­мость абсолютной магнитной проницаемости

от напряженности Я магнитного поля, кото­рая показана на рис. 6.7 пунктиром.

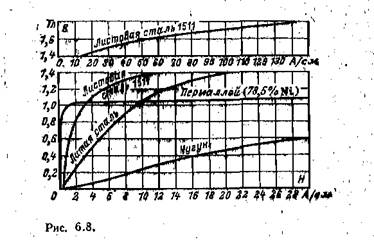
На рис. 6.8 приведены основные кривые намагничивания некоторых электротехниче­ских сталей, используемых в электрических машинах, трансформа­торах и других устройствах, чугуна и пермаллоя.

Из ферромагнитных материалов с линейными свойствами изготов­ляют участки магнитопроводов для катушек индуктивности колеба­тельных контуров с высокой добротностью. Такие контуры применяются

ются в различных радиотехнических устройствах (приемниках, пере­датчиках), в малогабаритных антеннах средств связи и т. д.

Если участок магнитопровода с площадью поперечного сечения 5 нельзя считать тонкостенным, то расчет часто все же можно вести, пользуясь средними значениями индукции В_ср = Ф/S и напряжен­ности H_Ср магнитного поля (на средней магнитной линии). Например, для тороида с прямоугольной формой поперечного сечения, внутрен­ним радиусом г_ь внешним радиусом г_± и высотой \1 изготовленного из

магнитного материала с линейными свойствами, т. е. при В = (см. рис. 6.6,),

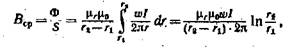
В дальнейшем для упрощения расчетов неоднородность магнит­ного поля в поперечном сечении каждого участка магнитопровода учитывать не будем и будем считать, что поле в каждом участке одно­родное и определяется значениями напряженности и индукции на сред­ней магнитной линии.

Дата добавления: 2015-08-02