Предел функции на бесконечности (по Гейне и по Коши).

(К) Число B называется пределом функции У = F(Х) при Х®¥, если для любого положительного числа e найдется отвечающее ему положительное число d, зависящее от e, такое, что для всех значений аргумента Х, удовлетворяющего условию |X|>d, справедливо неравенство |F(X) – B|<e. ("e>0)($ d=d(e)>0)("xÎX:|x|>d):|F(x) – B|<e

(Г) Число B называется пределом функции У = F(Х) при Х®+¥ (при Х® - ¥), если для любой бесконечно большой последовательности значений аргумента {Хn}, все элементы которой положительны (отрицательны), соответствующая последовательность значений функции {F(Xn} сходится к числу B.

("{Xn} – б-б, XnÎX, Xn>0):{F(Xn)}®B

("{Xn} – б-б, XnÎX, Xn<0):{F(Xn)}®B

(К) Число B называется пределом функции У = F(Х) при Х®+¥ (при Х®- ¥), если для любого положительного числа e найдется отвечающее ему положительное число d, зависящее от e, такое, что для всех значений аргумента Х, удовлетворяющего условию X>d (X<d), справедливо неравенство |F(X) – B|<e.

("e>0)($ d=d(e)>0)("xÎX:x>d):|F(x) – B|<e

("e>0)($ d=d(e)>0)("xÎX:x<d):|F(x) – B|<e

20. Теорема о пределах функции.

ТЕОР: Пусть две функции f(x) и g(x) заданы на одном множестве и имеют пределы в точке А, равные В и С. Тогда функции f(x)+g(x), f(x) – g(x), f(x)*g(x), f(x)/g(x) имеют в точке А пределы равные В+С, В – С, В*С, В/С (при С¹0).

Док-во: Пусть {Xn} – произвольная, сходящаяся к А последовательность, все элементы которой отличны от А. Последовательности {f(Xn)} и {g(Xn)} сходятся к пределам В и С (опр. предела Ф. по Г). Тогда последовательности {f(Xn)+g(Xn)}, {f(Xn) – g(Xn)}, {f(Xn)·g(Xn)}, {f(Xn)/g(Xn)} сходятся к пределам В+С, В – С, В·С, В/С (С¹0). Þ Функции f(x)+g(x), f(x) – g(x), f(x)·g(x), f(x)/g(x) имеют в точке А пределы равные В+С, В – С, В·С, В/С (С¹0).

ТЕОР: Пусть функции f(x), g(x) и h(x) определены в некоторой окрестности точки А, за исключением, быть может, самой точки А, и функции f(x) и h(x) имеют предел в точке А, равный В. Пусть, кроме того, выполняется неравенство f(x)£g(x) £h(x) для всех хÎХ. Тогда предел функции g(x) в точке А равен В.

Док-во: Пусть {Xn} – произвольная, сходящаяся к А последовательность значений аргумента функций f(x) и h(x), все элементы которой отличны от А. Последовательности {f(Xn)} и {h(Xn)} сходятся к пределу В. Используя неравенства f(x)£g(x) £h(x) для "nÎN. Но тогда последовательность {g(Xn)} сходятся к пределу В. Þ lim g(x)=B в точке А.

21. I замечательный предел.

ТЕОР: Предел функции g(x) = sinx\x в точке х = 0 существует и равен 1, т.е. limsinx\x=1 (n®¥)

Док-во: Рассмотрим дугу окружности радиуса R=1 с центральным углом, радиальная мера которого равна Х (0<X<p/2).

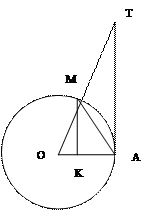Тогда АО=1, sin X=MK, tg X=AT.

Площадь треугольника ОАМ меньше площади сектора ОАМ, которая меньше площади треугольника ОАТ, или 1/2ОА·МК<1/2OA·AM<1/2OA·AT Þ1/2sin X<1/2X<1/2tg X Þ sin X<X<tg X. Разделим эти неравенства на sin X>0, получим 1<x\sinx<1\cosx. Для обратных величин справедливы обратные неравенства cosX<sinx\x<1.

Так как неравенства справедливы при 0<X<p/2 Þ они справедливы и при -p/2<X<0, так как при замене Х на –Х все три функции cosX, (sin X)/X и 1 не меняют своих значений. Т. о. неравенства справедливы при всех ХÎ(-p/2, p/2), за исключением точки Х=0.

Так как обе функции f(x)=cosX и h(x)=1 имеют в точке Х=0 предел равный 1, то g(x)= sinx\x тоже имеет в точке Х=0 предел равный 1.

22. II замечательный предел.

ТЕОР: Предел функции f(x) = (1+1\x)^x при х®¥ существует и равен числу е, т.е. lim(1+1\x)^x= e.(х®¥)

Док-во: Пусть X>1.

Положим n=[x] (целая часть Х), тогда X=n+a, где n – натуральное число, а a удовлетворяет условию 0£a<1. Так как n£X<n+1, 1/(n+1)<1/X£1/n и 1+1/(n+1)<1+1/X£1+1/n, то (по свойству возрастания показательной Ф. с основанием, большим 1) (1+1\(n+1))^n<(1+1\x)^x<(1+1\n)^(n+1). При Х®+¥ (n®¥) lim(1+1\n)^(n+1)=lim(1+1+n)^n·lim(1+1\n)=e·1=e и lim(1+1\(n+1))^n=[lim(1+1\(n+1))^(n+1)]/[lim(1+1\(n=1)]=e. Þ lim(1+1\x)^x=e.

Пусть теперь X<-1, X= -Y.

Тогда lim(1+1\x)^x=lim(1-1\y)^-y=lim(1_1(y-1))^y=lim(1+1(y-1))&(y-1)·lim(1+1\(y+1)= e·1=e

(при X® -¥, Y® +¥).

Окончательно имеем lim(1+1\x)^x= e.

23. Бесконечно малые функции. Действия над ними.

Функция называется бесконечно малой в точке х=А (или при х®А), если предел этой функции в точке А равен 0.

(К) Функция a(х) называется бесконечно малой в точке х=А (или при х®А), если для любого положительного числа e >0 существует d>0 такое, что для всех хÎХ, удовлетворяющих условию 0<|x – A|<d, выполняется неравенство |a(x)|<e.

("e>0)($d=d(e)>0)("xÎX,0<|x – A|<d):|a(x)|<e

(Г) Функция a(х) называется бесконечно малой в точке х=А (или при х®А), если для любой сходящейся к А последовательности {Xn} значений аргумента Х, отличных от А, соответствующая последовательность значений функции {a(Xn)} является бесконечно малой. ("{Xn}®A, Xn¹A):{F(Xn)} – б-м

ТЕОР: Для выполнения равенства limf(x)=b (х®¥)необходимо и достаточно, чтобы функция

a(х)=f(х) - b была бесконечно малой при х®a.

Док-во:Необходимость: пусть limf(x)=b. Рассмотрим разность a(х)=f(х) – b и докажем, что a(х) – бесконечно малая функция при х®a. Действительно lim a(х)=lim(f(х) – b)=limf(x) – lim b=b – b=0.

Достаточность: Пусть a(х)=f(х) – b, где a(х) – бесконечно малая функция при х®a. Докажем, что limf(x)=b. Так как f(x)=b+a(х), то limf(x)= lim(b+a(х))= lim b+ lim a(х) =b+0=b.

ТЕОР: Алгебраическая сумма и произведение конечного числа бесконечно малых функций при х®а, а также произведение бесконечно малой функции на ограниченную являются бесконечно малыми функциями при х®а.

Док-во: Вытекает из определения предела функции по Гейне и свойств бесконечно малых последовательностей.

Дата добавления: 2015-08-02