Геометрический смысл производной.

Пусть функция Y=f(x) определена на интервале (a, b) и пусть точка А на графике функции соответствует значению аргумента Х0, а точка В – значению (Х0+DХ). Проведем через А и В прямую и назовем ее секущей. Обозначим через j(DХ) угол между секущей и осью ОХ.

Если при DХ®0 существует lim j(DX)= j 0, то прямую с угловым коэффициентом К=tg j 0, проходящим через точку А(Х0, f(X0)), называют предельным положением секущей АВ при DХ®0 (или В®А).

Касательной S к графику функции Y=f(x) в точке А будем называть предельное положение секущей АВ при DХ®0 (или при В®А).

ТЕОР: Если функция Y=f(x) имеет в точке Х0 производную, то существует касательная к графику Y=f(x) в точке М(X0, f(X0)), угловой коэффициент касательной K=tg j 0 = f ’(X0).

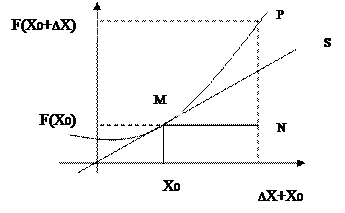Док-во: Проведем прямую MN || OX, тогда PN || OY, MN=DX, PN=DY, ÐPMN=j => tg j(DX) = DY/DX = (f(x0-DX)-f(x0))\ DX Þ j(DX) =arctg DY/DX. Перейдем к пределу при DX®0. Так как существует производная f ’(X0), то существует и предел lim DY/DX=f ’(X0) и так как функция arctg DY/DX непрерывна Þ существует предел правой части равенства:

lim arctg DY/DX= arctg (lim DY/DX)=arctg f ’(X0). Þ Существует предел и левой части равенства. Получаем lim j(DX) = arctg f ’(X0). Þ Существует предельное положение секущей РМ, т. е. существует касательная к графику функции Y=f(x) в точке А(X0, f(X0)), причем угол наклона этой касательной к оси ОХ равен arctg f ’(X0) и, значит, угловой коэффициент касательной tg j 0= f ’(X0).

Составим уравнение касательной к графику функции Y=f(x) в точке A(X0, f(X0)). Уравнение прямой, проходящей через точку C(a, b) с угловым коэффициентом k имеет вид Y=b+k(x –a). Но в точке А значение функции равно f(X0), поэтому в уравнении а=Х0, b= f(X0), k= f ’(X0). Получаем уравнение касательной Y= f(X0)+ f ’(X0)(X - X0).

Геометрический смысл производной состоит в том, что значение производной функции в точке равно угловому коэффициенту касательной в этой точке.

35. Понятие дифференцируемости функции.

Функция Y=f(x) называется дифференцируемой в точке X0, если ее приращение DY в этой точке можно представить в виде DY=A·DX+a(DX)·DX, где А – некоторое число, не зависящее от DX, а a(DX) – функция аргумента DX, являющаяся бесконечно малой при DX®0, т. е. lim a(DX)=0.

ТЕОР: Для того, чтобы функция Y=f(x) была дифференцируема в точке X0, необходимо и достаточно, чтобы она имела в этой точке конечную производную.

Док-во:Необходимость: Пусть функция Y=f(x) дифференцируема в точке X0, т. е. ее приращение представимо в виде DY=A·DX+a(DX)·DX. Поделим это равенство на DX, получим DY/DX=А+a(DX). Переходя к пределу при DX®0, имеем lim (DY/DX)=lim (А+a(DX))=A. Þ Производная в точке X0 существует и f ’(X0)=А.

Достаточность: Пусть существует конечная производная f ’(X0), т. е. lim (DY/DX)= f ’(X0). Обозначим f ’(X0)=А, тогда функция a(DX)=DY/DX - А является бесконечно малой при DX®0. Из последнего равенства имеем DY=A·DX+a(DX) ·DX, где lim a(DX)=0. Получено представление DY=A·DX+a(DX)·DX. Þ Функция Y=f(x) дифференцируема в точке X0.

Дата добавления: 2015-08-02