Дисперсия и поглощение света

• Согласно элементарной теории дисперсии диэлектрическая проницаемость
вещества:

где л₄ — концентрация электронов с собственной частотой и>_ок.

• Связь между показателем преломления и диэлектрической проницае­
мостью вещества:

n=Ji. (4.56)

• Фазовая и и групповая и скорости:

v = ш/к, и = da/dk. (4.5 в)

• Формула Рэлея:

и = v - Xdv/dX. (4.5 г)

• Закон ослабления узкого пучка электромагнитного излучения:

/ = /„ехр (-,.<*), (4.5 д)

где м⁼х⁺х'; М>*.*' - линейные показатели ослабления, поглощения и рассеяния.

4.228. Электромагнитная волна с частотой ы распространяет­
ся в разреженной плазме. Концентрация свободных электронов
в плазме равна и₀. Пренебрегая взаимодействием волны с
ионами плазмы, найти зависимость:

а) диэлектрической проницаемости плазмы от частоты;

б) фазовой скорости от длины волны А. в плазме.

4.229. Найти концентрацию свободных электронов ионо­
сферы, если для радиоволн с частотой v = 100 МГц ее показа­
тель преломления п = 0,90.

4.230. Имея в виду, что для достаточно жестких рентгенов­
ских лучей электроны вещества можно считать свободными,
определить, на сколько отличается от единицы показатель
преломления графита для рентгеновских лучей с длиной волны
в вакууме Л = 50 пм.

4231. Электрон, на который действует квазиупрутая сила кх
и "сила трения" ух, находится в поле электромагнитного
излучения. Электрическая составляющая поля меняется во
времени по закону Е = E₀cosu>t. Пренебрегая действием магнит­
ной составляющей поля, найти:

а) уравнение движения электрона;

б) среднюю мощность, поглощаемую электроном; частоту,
при которой она будет максимальна; выражение для макси­
мальной средней мощности.

4232. В ряде случаев диэлектрическая проницаемость
вещества оказывается величиной комплексной или отрицатель­
ной и показатель преломления - соответственно комплексным
(n'=n + ix). Написать для этих случаев уравнение плоской
волны и выяснить физический смысл таких показателей
преломления.

4233. При зондировании разреженной плазмы радиоволнами
различных частот обнаружено, что радиоволны с частотами
v < v₀ = 400 МГц не проходят через плазму. Найти концентрацию
свободных электронов в этой плазме.

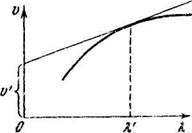
4234. Исходя из определения групповой скорости и = du/dk,
получить формулу Рэлея (4.5 г). Показать также, что значение
и вблизи X = к' равно отрезку и', отсекаемому касательной к
кривой и (Я) в точке X' (рис. 4.40).

4235. Найти зависимость

между групповой и и фазовой и скоростями для следующих зако­нов дисперсии:

а) и<ч>1/^Х; 6)v<*k; b)ikn>1/v²,

где Л, к и v - длина волны, волновое число и частота.

Рис. 4.40

4.236. В некоторой среде связь между групповой и фазо­вой скоростями электромагнит­ной волны имеет вид ии = с², где с — скорость света в вакуу­ме. Найти зависимость диэлектрической проницаемости этой

среды от частоты волны e(w).

4J37. Показатель преломления сероуглерода для света с длинами волн 509, 534 и 589 нм равен соответственно 1,647, 1,640 и 1,630, Вычислить фазовую и групповую скорости света

вблизи к = 534 нм.

4J38. Плоский световой импульс распространяется в среде, где фазовая скорость линейно зависит от длины волны как v=a+bX, а и Ь - некоторые положительные постоянные. Показать, что в такой среде форма произвольного светового импульса будет восстанавливаться через промежуток времени

4J39. Пучок естественного света интенсивности 7₀ падает на систему из двух скрещенных поляризаторов, между которыми находится трубка с оптически неактивным раствором в продольном магнитном поле напряженности Н. Длина трубки /, линейный показатель поглощения раствора к и постоянная Верде V. Пренебрегая отражениями, найти интенсивность света, прошедшего через эту систему.

4.240. Плоская монохроматическая световая волна интенсив­
ности /₀ падает нормально на пластинку толщины d с
линейным показателем поглощения х. Коэффициент отражения
каждой поверхности пластинки равен р. Найти интенсивность
прошедшего света:

а) пренебрегая вторичными отражениями;

б) учитывая многократные отражения.

4.241. Из некоторого вещества изготовили две пластинки:
одну толщины dj = 3,8 мм, другую толщины dj = 9,0 мм. Введя
поочередно эти пластинки в пучок монохроматического света,
обнаружили, что первая пластинка пропускает т ₁ = 0,84 светового

потока, а вторая х₂ =0,70. Найти линейный показатель поглоще­ния этого вещества. Свет падает нормально. Вторичными отражениями пренебречь.

4242. Световой пучок проходит через стопу из ЛГ = 5
одинаковых пластинок, каждая толщины / = 5,0 мм. Коэффици­
ент отражения каждой поверхности р =0,050. Отношение
интенсивности света, прошедшего через эту систему, к интен­
сивности падающего света т=0,55. Пренебрегая вторичными
отражениями, определить линейный показатель поглощения
данного стекла.

4243. Свет падает нормально на поверхность пластины
толщины /. Показатель поглощения вещества пластины
линейно изменяется вдоль нормали к ее поверхности от х_х до
к₂. Коэффициент отражения каждой поверхности пластины р.
Пренебрегая вторичными отражениями, найти коэффициент
пропускания пластины.

4244. Пучок света интенсивности /₀ падает нормально на
прозрачную пластинку толщины /. Пучок содержит все длины
волн в диапазоне от А_х до А₂ одинаковой спектральной
интенсивности. Найти интенсивность прошедшего через
пластинку пучка, если в этом диапазоне длин волн показатель
поглощения линейно зависит-от А в пределах от х_х до х₂ и
коэффициент отражения каждой поверхности равен р. Вторич­
ными отражениями пренебречь.

4245. Светофильтром является пластинка толщины d с
линейным показателем поглощения, зависящим от длины

волны А как к = а(1 -А/А_о)², где а и А_о - постоянные. Найти ширину полосы пропускания ДА этого светофильтра, при которой ослабления света на краях полосы в ц раз больше, чем при А_о. Коэффициент отражения поверхностей считать одинаковым для всех длин волн. Вторичными отражениями пренебречь.

4246. Точечный изотропный источник, испускающий
световой поток Ф, находится в центре сферического слоя
вещества, внутренний радиус которого а, наружный Ь. Линей­
ный показатель поглощения вещества к, коэффициент отраже­
ния поверхностей р. Пренебрегая вторичными отражениями,
найти интенсивность света на выходе из этого слоя.

4247. Во сколько раз уменьшится интенсивность узкого
пучка рентгеновского излучения с длиной волны 20 пм при
прохождении свинцовой пластинки толщины d = 1,0 мм, если

массовый показатель ослабления для данной длины волны ц/р = 3,6 см²/г?

4.248. Узкий пучок рентгеновского излучения с длиной волны 62 пм проходит через алюминиевый экран толщины 2,6 см. Какой толщины свинцовый экран будет ослаблять данный пучок в такой же степени? Массовые показатели ослабления алюминия и свинца для этого излучения равны соответственно 3,48 и 72,0 см²/г.

4249. Найти для алюминия толщину слоя половинного
ослабления узкого пучка монохроматического рентгеновско­
го излучения, если массовый показатель ослабления

ji/p = 0,32 см²/г.

4250. Сколько слоев половинного ослабления в пластинке,
которая уменьшает интенсивность узкого пучка рентгеновского
излучения в ц =50 раз?

Часть 5 КВАНТОВАЯ ФИЗИКА

Дата добавления: 2015-08-02