Читайте также:
|
Опр. Системой координат в аффинном пространстве 
называют набор 
, в котором o – точка из A, а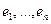 
- базис 
. o – начало координат. Т.к.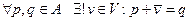 
, то можно определить координаты точки p в фиксированной системе координат, как набор 
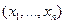, где x – координаты в разложении вектора 
по базису. Систему координат также можно задать 
точкой в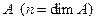 
. При этом 
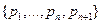- система координат с началом в 
и базисными векторами 
.
26.03.05
Дата добавления: 2015-07-21; просмотров: 38 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Изоморфизм | | | Сущность унитарного предприятия |