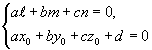Общее уравнение плоскости
ax + by + cz + d = 0;
если а = 0, плоскость параллельна прямой Ох; если b = 0, плоскость параллельна прямой Оy; если c = 0, плоскость параллельна прямой Oz; если d = 0, плоскость проходит через начало координат; если a = b = 0, плоскость параллельна плоскости xОy; если a = c = 0, плоскость параллельна плоскости xОz; если b = c = 0, плоскость параллельна плоскости yОz;
Уравнение прямой в отрезках:
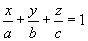 а, b, с — отрезки, отсекаемые плоскостью на осях;
Уравнение прямой, проходящей через точку А(х0; у0; z0) перпендикулярно вектору
а, b, с — отрезки, отсекаемые плоскостью на осях;
Уравнение прямой, проходящей через точку А(х0; у0; z0) перпендикулярно вектору 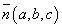 :
а(х – х0) + b(у – у0) + с (z – z0) = 0
Угол между плоскостями а1х + b1y + c1z + d1= 0 и а2х + b2y + c2z + d2= 0 :
а(х – х0) + b(у – у0) + с (z – z0) = 0
Угол между плоскостями а1х + b1y + c1z + d1= 0 и а2х + b2y + c2z + d2= 0
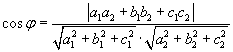 Условие параллельности двух плоскостей
Условие параллельности двух плоскостей
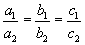 Условие перпендикулярности двух плоскостей
а1а2 + b1b2 + c1c2 = 0
Расстояние от точка М0(х0; у0; z0) до плоскости ax + by + cz + d = 0
Условие перпендикулярности двух плоскостей
а1а2 + b1b2 + c1c2 = 0
Расстояние от точка М0(х0; у0; z0) до плоскости ax + by + cz + d = 0
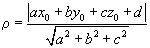 Уравнение прямой в пространстве
канонические уравнения прямой, проходящей через точку М0 (х0; у0; z0) параллельно вектору
Уравнение прямой в пространстве
канонические уравнения прямой, проходящей через точку М0 (х0; у0; z0) параллельно вектору 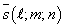 : :
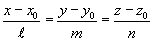 проходящей через две точки М1 (х1; у1; z1) и М2 (х2; у2; z2):
проходящей через две точки М1 (х1; у1; z1) и М2 (х2; у2; z2):
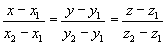 уравнение прямой — линии пересечения плоскостей:
уравнение прямой — линии пересечения плоскостей:
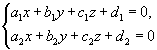 Угол между прямыми
Угол между прямыми 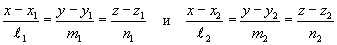
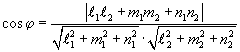 Условие параллельности двух прямых
Условие параллельности двух прямых
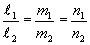 Условие перпендикулярности двух прямых
Условие перпендикулярности двух прямых
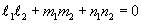 Угол между прямой
Угол между прямой 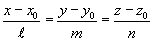 и плоскостью ax + by + cz + d = 0 и плоскостью ax + by + cz + d = 0
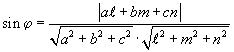 Условие параллельности прямой и плоскости
Условие параллельности прямой и плоскости
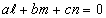 Условие перпендикулярности прямой и плоскости
Условие перпендикулярности прямой и плоскости
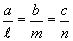 Условие принадлежности прямой плоскости
Условие принадлежности прямой плоскости
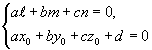
|

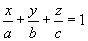 а, b, с — отрезки, отсекаемые плоскостью на осях;
Уравнение прямой, проходящей через точку А(х0; у0; z0) перпендикулярно вектору
а, b, с — отрезки, отсекаемые плоскостью на осях;
Уравнение прямой, проходящей через точку А(х0; у0; z0) перпендикулярно вектору 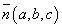 :
а(х – х0) + b(у – у0) + с (z – z0) = 0
Угол между плоскостями а1х + b1y + c1z + d1= 0 и а2х + b2y + c2z + d2= 0
:
а(х – х0) + b(у – у0) + с (z – z0) = 0
Угол между плоскостями а1х + b1y + c1z + d1= 0 и а2х + b2y + c2z + d2= 0
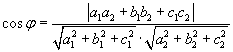 Условие параллельности двух плоскостей
Условие параллельности двух плоскостей
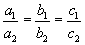 Условие перпендикулярности двух плоскостей
а1а2 + b1b2 + c1c2 = 0
Расстояние от точка М0(х0; у0; z0) до плоскости ax + by + cz + d = 0
Условие перпендикулярности двух плоскостей
а1а2 + b1b2 + c1c2 = 0
Расстояние от точка М0(х0; у0; z0) до плоскости ax + by + cz + d = 0
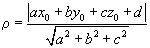 Уравнение прямой в пространстве
канонические уравнения прямой, проходящей через точку М0 (х0; у0; z0) параллельно вектору
Уравнение прямой в пространстве
канонические уравнения прямой, проходящей через точку М0 (х0; у0; z0) параллельно вектору 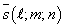 :
:
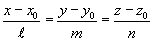 проходящей через две точки М1 (х1; у1; z1) и М2 (х2; у2; z2):
проходящей через две точки М1 (х1; у1; z1) и М2 (х2; у2; z2):
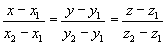 уравнение прямой — линии пересечения плоскостей:
уравнение прямой — линии пересечения плоскостей:
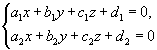 Угол между прямыми
Угол между прямыми 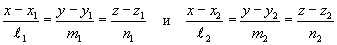
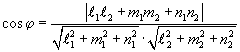 Условие параллельности двух прямых
Условие параллельности двух прямых
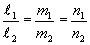 Условие перпендикулярности двух прямых
Условие перпендикулярности двух прямых
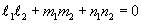 Угол между прямой
Угол между прямой 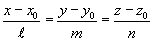 и плоскостью ax + by + cz + d = 0
и плоскостью ax + by + cz + d = 0
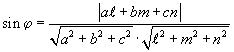 Условие параллельности прямой и плоскости
Условие параллельности прямой и плоскости
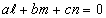 Условие перпендикулярности прямой и плоскости
Условие перпендикулярности прямой и плоскости
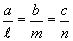 Условие принадлежности прямой плоскости
Условие принадлежности прямой плоскости