В декартовых координатах

Различают основные виды области интегрирования.

1. Областью интегрирования является прямоугольник: область D ограничена слева и справа прямыми x = a и x = b, а снизу и сверху – прямыми y = c и y = d (рис. 2).

Рис. 2

Для такой области двойной интеграл вычисляется по формуле

= = . (3)

2. Областью интегрирования является правильная замкнутая область D. (Область D называется правильной, если любые прямые, параллельные оси Ox или оси Oy пересекают область D не более, чем в двух точках.)

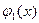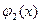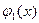
Область интегрировании D ограничена слева и справа прямыми x = a и x = b, а снизу и сверху непрерывными кривыми y= и y= ( 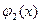) (рис.3), т.е.

D:

(4)

Рис. 3

Для такой области двойной интеграл вычисляется по формуле

= , (5)

причем сначала вычисляется внутренний интеграл 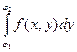, в котором x считается постоянным.

3. Правильная замкнутая область интегрирования D ограничена снизу и сверху прямыми y = c и y = d (c < d), а слева и справа – непрерывными кривыми x= и x= ( 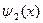) (рис.4), т.е.

D: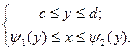

(6)

Рис. 4

Для такой области двойной интеграл вычисляется по формуле

= , (7)

причем сначала вычисляется внутренний интеграл , в котором y считается постоянным.

4. В случае неправильной области D двойной интеграл сводится к сумме интегралов:

= . (8)

При вычислении двойных интегралов необходимо помнить, что:

1. Пределы внешнего интеграла в повторном всегда постоянны. Отрезком интегрирования является проекция правильной области интегрирования D на соответствующую координатную ось.

2. Пределы внутреннего интеграла являются функциями переменной интегрирования внешнего интеграла.

3. В повторном интеграле сначала вычисляется внутренний интеграл, а затем внешний.

4. При вычислении внутреннего интеграла переменная, по которой берется внешний интеграл, рассматривается как постоянная. Его пределы рассматриваются длянего также как постоянные.

5. В случае области (4), если кривая y= 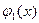или y= 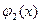в промежутке a x b задается несколькими аналитическими выражениями, то двойной интеграл сводится к сумме повторных интегралов, в каждом из которых функция y= 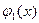или y= 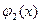задается одним аналитическим выражением. Аналогично для области (6).

Дата добавления: 2015-07-20