
Читайте также:
|
3.1. Изобразим область интегрирования D (рис. 9).
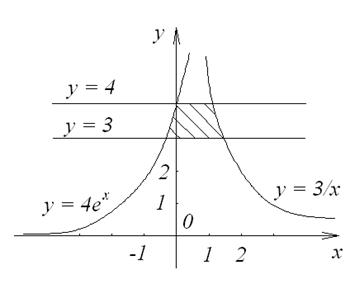
Рис. 9
Область интегрирования принадлежит к виду (6) (см. п.2).
Выразим x из уравнений 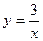 и
и 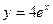 :
: 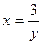 и
и 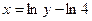 .
.
Тогда область D определяется системой неравенств:
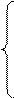
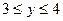 ,
,
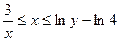 .
.
Для вычисления площади фигуры используем формулу (11).
 S =
S = 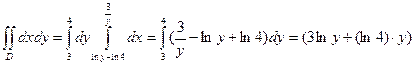
 –
– 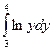 .
.
Вычислим
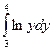 =
= 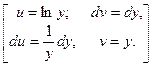 =
= 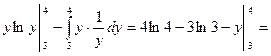
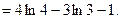
Тогда
S = 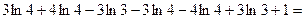 1 (кв.ед.).
1 (кв.ед.).
Ответ: 1 кв.ед.
3.2. Преобразуем данные уравнения окружностей:
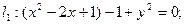
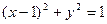 – уравнение окружности (C (1,0), R = 1);
– уравнение окружности (C (1,0), R = 1);
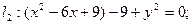
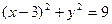 – уравнение окружности (C (3,0), R = 3).
– уравнение окружности (C (3,0), R = 3).
Изобразим область интегрирования D (рис. 10).
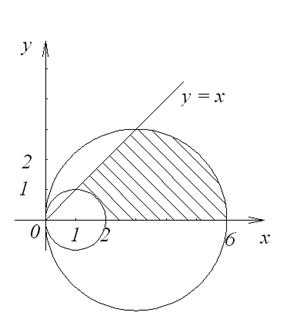
Рис. 10
Т.к. 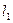 и
и 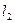 являются окружностями, то лучше перейти к полярным координатам.
являются окружностями, то лучше перейти к полярным координатам.
Переводим уравнения окружностей в полярные координаты, используя формулы: 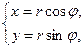 тогда, подставляя соответственно в (16) и (17), получим:
тогда, подставляя соответственно в (16) и (17), получим:
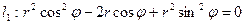 ,
,
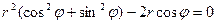 ,
,
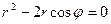 ,
,
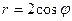 .
.
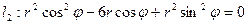 ,
,
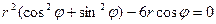 ,
,
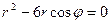 ,
,
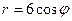 .
.
Область D определяется системой неравенств:

Для вычисления площади фигуры используем формулу (11), а также формулу (9) для преобразования двойного интеграла от прямоугольных координат к полярным.
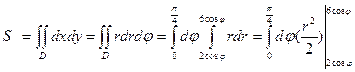 =
= 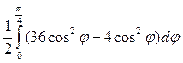 =
=
= 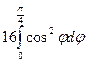 =
= 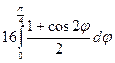 = 8(
= 8(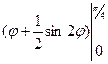 =
= 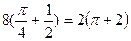 .
.
Ответ: 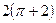 (кв. ед.).
(кв. ед.).
Дата добавления: 2015-07-20; просмотров: 46 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Решение. | | | ЗАДАЧИ ДЛЯ САМОПОДГОТОВКИ |