Основные понятия и определения. Методические указания

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К РЕШННИЮ ЗАДАЧ ПО ТЕМЕ

"ДВОЙНЫЕ ИНТЕГРАЛЫ"

для студентов специальности 270105

"Городское строительство и хозяйство"

Сочи ± СГУТиКД ± 2011

УДК 517

ББК 22.16

Г67

Рекомендовано к печати на заседании кафедры прикладной математики

Сочинского государственного университета туризма и курортного дела

(протокол № 11 от 19.03.2011)

Рецензент:

канд. техн. наук, доцент И.Л. Макарова

Составитель:

ст. преподаватель О.Ю. Горлова

Методические указания к решению задач по теме "Двойные интегралы": Г67 учебно-методическое издание. - Сочи: РИЦ СГУТиКД, 2011.-26 с.

Методические указания содержат примеры решения задач и задачи для самостоятельной работы по теме "Двойные интегралы".

Примеры решения задач предваряются вводным справочным материалом и основными формулами.

Рекомендуется для использования студентами инженерных специальностей всех форм обучения.

УДК 517

© Сочинский государственный университет

туризма и курортного дела, 2011

© Горлова О. Ю., составление, 2011

СОДЕРЖАНИЕ

Предисловие
1. Основные понятия и определения.............................................................................
2. Вычисление двойного интеграла в декартовых координатах................................
3. Вычисление двойного интеграла в полярных координатах...................................
4. Приложения двойного интеграла..............................................................................
5. Примеры решения задач.............................................................................................
6. Задачи для самоподготовки.......................................................................................
ПРИЛОЖЕНИЕ 1.Таблица основных интегралов......................................................
Рекомендуемая литература............................................................................................

ПРЕДИСЛОВИЕ

В настоящем пособии содержатся определения, формулы, другие краткие сведения по теории, методические указания, необходимые для решения последующих задач; приводятся подробные решения типичных задач с пояснениями теоретических положений. В пособие также включены задачи для самостоятельного решения с ответами к ним.

Содержание методических указаний соответствует учебному плану по дисциплине "Математика" для студентов специальности 270105 "Городское строительство и хозяйство".

Детально разобранные примеры задач имеют цель помочь студентам глубже освоить теоретический материал, подготовиться к выполнению лабораторных работ. Самостоятельное выполнение приведенных задач обеспечит успешную подготовку к экзаменационной сессии по данному разделу.

ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

Обобщением определенного интеграла на случай функций двух переменных является так называемый двойной интеграл.

Пусть в замкнутой области D плоскости Oxy задана непрерывная функция z = f(x,y).

Рис. 1

Разобьем эту область произвольным способом на n частичных областей с площадями , , …, . Диаметры этих областей обозначим , , …, . (Диаметром области называется наибольшее из расстояний между двумя точками границы этой области.) Выберем в каждой элементарной области произвольную точку и умножим значение функции в точке на площадь этой области.

Интегральной суммой для функции f(x,y) по области D называется сумма вида

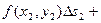… + . (1)

Если при неограниченном увеличении n (n , max ) интегральная сумма имеет определенный конечный предел

I = , не зависящий от способа разбиения D на элементарные области и от выбора точек в пределах каждой из них, то этот предел называется двойным интегралом от функции f(x,y) в области D и обозначается следующим образом:

I = = . (2)

Двойной интеграл обладает всеми основными свойствами обыкновенного определенного интеграла: область интегрирования двойного интеграла можно разбивать на части, двойной интеграл от суммы функций равен сумме двойных интегралов от всех слагаемых, постоянный множитель можно выносить за знак двойного интеграла.

Дата добавления: 2015-07-20