
Читайте также:
|
Приведем некоторые примеры применения двойного интеграла.
1. Объем тела,
Объем цилиндрического тела, ограниченного сверху поверхностью z=f(x,y) 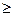 0, снизу – замкнутой областью D плоскости Oxy, с боков - цилиндрической поверхностью, образующая которой параллельна оси Oz, а направляющей служит граница области D (рис. 1) находится по формуле
0, снизу – замкнутой областью D плоскости Oxy, с боков - цилиндрической поверхностью, образующая которой параллельна оси Oz, а направляющей служит граница области D (рис. 1) находится по формуле
V = 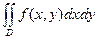
| (10) |
2. Площадь плоской фигуры.
Площадь S области D вычисляется по формуле
S = 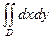 . .
| (11) |
3. Масса плоской фигуры.
Масса плоской пластинки D с переменой плотностью 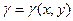 находится по формуле
находится по формуле
m = 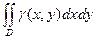 . .
| (12) |
4. Статические моменты и координаты центра тяжести плоской фигуры.
Статические моменты фигуры D относительно осей Ox и Oy могут быть вычислены по формулам
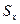 = = 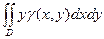 и и 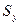 = = 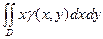
| (13) |
где 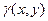 – переменная плотность; а координаты центра масс фигуры – по формулам
– переменная плотность; а координаты центра масс фигуры – по формулам
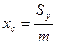 ; ; 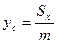 . .
| (14) |
5. Моменты инерции плоской фигуры.
Моменты инерции плоской фигуры относительно осей Ox и Oy могут быть вычислены по формулам:
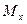 = = 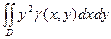 и и 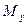 = = 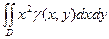
| (15) |
где 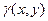 – переменная плотность.
– переменная плотность.
Момент инерции фигуры относительно начала координат – по формуле
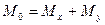 . .
| (16) |
Дата добавления: 2015-07-20; просмотров: 51 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| В ПОЛЯРНЫХ КООРДИНАТАХ | | | Решение. |