
Читайте также:
|
Указание. В случае затруднений при вычислении интегралов можно воспользоваться "Таблицей основных интегралов" (Приложение 1).
1. Изменить порядок интегрирования (сделать чертеж области):
1.1 
 ;
;
1.2. 
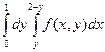 ;
;
1. 3. 
 +
+  ;
;
1. 4. 
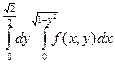 +
+  ;
;
1. 5. 
 +
+  ;
;
1. 6. 
 .
.
2. Вычислить двойной интеграл по области D, ограниченной заданными линиями. Сделать чертеж.
2.1. I =  , где область D, ограничена линиями y = x, y = 3 x,
, где область D, ограничена линиями y = x, y = 3 x,
x = 1, x = 3;
2.2. I =  , где область D, ограничена линиями x = 1,
, где область D, ограничена линиями x = 1,
 ;
;
2.3. I =  , где область D, ограничена линиями y = x, y =
, где область D, ограничена линиями y = x, y =  , x = 1, x = 2;
, x = 1, x = 2;
2.4. I =  , где область D, ограничена линиями x = 0, y = 0, y = 4 – x;
, где область D, ограничена линиями x = 0, y = 0, y = 4 – x;
2.5. I =  , где область D, ограничена линиями y =
, где область D, ограничена линиями y =  ,
,
y =  , x = 0.
, x = 0.
3. С помощью двойного интеграла вычислить площадь фигуры, ограниченной заданными линиями (сделать чертеж):
3.1.  ; y = x.
; y = x.
3.2. x = 0; y =  ; y = 4 – (x – 1)
; y = 4 – (x – 1)  .
.
3.3. 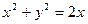 ;
;  ; y = x; y = 0.
; y = x; y = 0.
3.4.  ;
;  .
.
3.5.  ; y = – 1; y = – x.
; y = – 1; y = – x.
3.6.  ; 2 x - 4 y + 1 = 0.
; 2 x - 4 y + 1 = 0.
3.7. y = 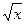 ; y = 2
; y = 2 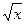 ; x = 4.
; x = 4.
3.8.  ; x – y = 1; y = -1.
; x – y = 1; y = -1.
3.9. 
4. Вычислить с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной кривой, заданной неявной функцией F (x,y) = 0; a > 0. Схематически изобразить фигуру.
4.1. 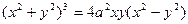 ;
;
4.2.  ;
;
4.3.  ;
;
4.4.  ;
;
4.5.  ;
;
4.6.  .
.
ОТВЕТЫ
1.1. 
 ; 1.2.
; 1.2. 
 +
+  ;
;
1.3. 
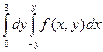 ; 1.4.
; 1.4. 
 +
+  ;
;
1.5. 
 ; 1.6.
; 1.6. 
 ; 2.1. 16; 2.2. 1; 2.3. 2,25;
; 2.1. 16; 2.2. 1; 2.3. 2,25;
2.4.  ; 2.5.
; 2.5.  ; 3.1.
; 3.1.  ; 3.2.
; 3.2. 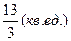 ; 3.3.
; 3.3.  ;
;
3.4. 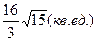 ; 3.5.
; 3.5.  ; 3.6.
; 3.6.  ; 3.7.
; 3.7.  ;
;
3.8.  ; 3.9.
; 3.9.  ; 4.1.
; 4.1.  ;
;
4.2.  ; 4.3.
; 4.3. 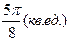 ; 4.4.
; 4.4.  ; 4.5.
; 4.5. 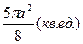 ;
;
4.6.  .
.
Приложение 1
ТАБЛИЦА ОСНОВНЫХ ИНТЕГРАЛОВ
 n/n
n/n
| Интеграл

| Инвариантная формула

|
| 1. | 
| 
|
| 2. | 
| 
|
| 3. | 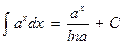
| 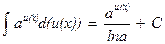
|
| 4. | 
| 
|
| 5. | 
| 
|
| 6. | 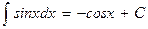
| 
|
| 7. | 
| 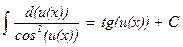
|
| 8. | 
| 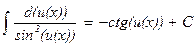
|
| 9. | 
| 
|
| 10. | 
| 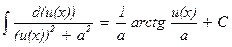
|
| 11. | 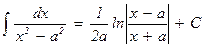
| 
|
| 12. | 
| 
|
| 13. | 
| 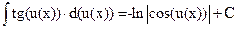
|
| 14. | 
| 
|
Продолжение приложения 1
| 15. | 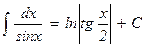
| 
|
| 16. | 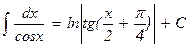
| 
|
| 17. | 
| 
|
| 18. | 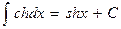
| 
|
| 19. | 
| 
|
| 20. | 
| 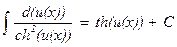
|
Рекомендуемая литература
1. Письменный Д.Т. Конспект лекций по высшей математике. 2 часть. – М.: Рольф, 2009. – 256с.
2. Лунгу К.Н., Норин В.П., Письменный Д.Т., Шевченко Ю.А. Сборник задач по высшей математике. – М.: Айрис – пресс, 2009. – 592 с.
3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2-х ч. Ч. II: Учебное пособие для втузов. – М.: ОНИКС, Мир и образование, 2009. – 448 с.
4. Соболь Б.В., Мишняков Н.Т., Поркшеян В.М. Практикум по высшей математике. – Ростов н/Д: Феникс, 2006. – 640 с.
5. Вербина Л.М., Самарин В.И. Высшая математика: Учебно-методическая разработка. В 4 ч. Ч. 3. - Сочи: СГУТиКД, 2002. - 79 с.
Учебно-методическое издание
Дата добавления: 2015-07-20; просмотров: 68 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Решение. | | | Из книги Р.Р. Камалетдинова «Идущим дорогой через ринг…», 2000 С.49-54 |