Эрмитовы операторы.

Опр. - эрмитов оператор в унитарном пространстве V, если (т.е. ).

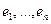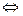Пусть - ортонормированный бзис V. - эрмитов оператор его матрица в в этом базисе эрмитова (этот факт был на самом деле доказан на предыдущей лекции).

Теорема. 1) Все собственные числа эрмитова оператора – вещественные.

2) Для эрмитова оператора существует ортонормированный базис из собственных векторов.

1) 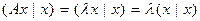, где x – собственный вектор. Но, с другой стороны, , откуда и следует .

2) Проведем индукцию по n. Для n=1 утверждение теоремы очевидно.

Шаг. Если , то доказывать нечего. Иначе - собственный вектор с собственным числом (вещественным по пред. пункту). Можно считать . Идея доказательства такая же, как и в вещественном случае. Обозначим через . Тогда W – подпространство, . (полное повторение вещественного случая, т.к. пространство решений одного уравнения). Покажем, что 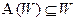. Действительно, () . Это и означает, что . По индукции в 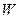есть ортонормированный базис из собственных векторов . Добавив к этой системе первым вектором x получим требуемый базис. .

Следствие. Для любой эрмитовой матрицы A существует унитарная матрица такая, что , где все .

Дата добавления: 2015-07-21