Ортогональность.

Эрмитово) скалярное произведение.

Пусть — комплексное пространство.

Определение. Скалярное произведение на — эрмитова положительно определённая форма. Обозначение: . Положительная определённость: из .

Ортогональность.

Пусть — унитарное пространство, то есть комплексное пространство со скалярным произведением.

Определение. и ортогональны, если .

Теорема. В конечномерном унитарном пространстве можно выбрать ортонормированный базис, т.е. .

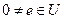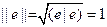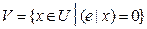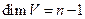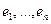Пусть — произвольный базис . Возьмём любой . Умножая на (вещественный) скаляр, можно считать . Пусть теперь . Тогда — уравнения с неизвестными . Так как , то — подпространство в , . По индукции () в есть ортонормированный базис . Положив, , получаем ортонормированный базис в .

Дата добавления: 2015-07-21