Унитарные операторы.

Пусть V – унитарное пространство, - линейный опреатор на нем.

Опр. - унитарный оператор, если .

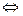Предложение. - унитарный оператор имеет унитарную матрицу в ортонормированном базисе.

Т.к. .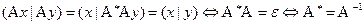

Теорема. Для любого унитарного оператора в конечномерном векторном унитарном пространстве существует ортонормированный базис, в котором он имеет матрицу вида

В частности, все собственные числа равны по норме единице.

(1) Пусть x - cобственный вектор с собственным числом . Тогда .

(2) Рассмотрим собственный вектор - его собственное значение. . Тогда выполнено инвариантно. Так как , то . По индукции взяв искомый базис в 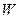и добавив и получим искомый базис всего пространства.

АФФИННЫЕ ТОЧЕЧНЫЕ ПРОСТРАНСТВА

Основное поле - .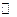

Опр. Пара , где - векторное пространство называется аффинным пространством, если задано отображение такое, что выполнено (под «+» подразумевается ):

1)

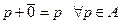
2)

3)

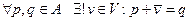
В последнем свойстве иногда пишут или . Элементы A называют точками аффинного пространства. Само аффинное простаранство называют ассоциированным с . Кроме того, говорят, что у аффинного пространства есть размерность:

Опр. Размерность А:

Дата добавления: 2015-07-21