
|
Читайте также: |
Пусть  — комплексная матрица
— комплексная матрица  .
.
Обозначим: 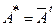 (
( — комплексное сопряжение).
— комплексное сопряжение).
Определение. Матрица  — эрмитова, если
— эрмитова, если 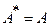 .
.
Матрица  — унитарная, если
— унитарная, если 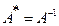 .
.
Теорема. Пусть  — матрица перехода от одного ортогонального базиса к другому ортогональному базису. Тогда
— матрица перехода от одного ортогонального базиса к другому ортогональному базису. Тогда  унитарна.
унитарна.
Пусть  — матрица перехода от
— матрица перехода от  к
к  . Если
. Если  , то
, то 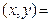
 . Если
. Если  — элементы
— элементы 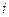 -ого столбца
-ого столбца  , то
, то  — элементы
— элементы 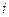 -ой строки у матрицы
-ой строки у матрицы  .
.
Произведение 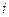 -ой строки
-ой строки  на
на  -ый столбец
-ый столбец  равно
равно  . Но это есть
. Но это есть  , так как
, так как  . Поэтому
. Поэтому  , так как базис
, так как базис  ортонормирован. Следовательно,
ортонормирован. Следовательно,  и
и  — унитарная матрица.
— унитарная матрица. 
6. Сопряжённый оператор.
Пусть  — унитарное пространство,
— унитарное пространство,  .
.
Определение.  — сопряжённый к
— сопряжённый к  , если
, если  .
.
Как и в вещёственном случае:  и
и  .
.
Теорема. Пусть  и
и  ,
, 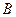 — матрицы
— матрицы  и
и 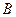 в ортонормированном базисе. Тогда
в ортонормированном базисе. Тогда 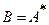 .
.
 .
. 
Дата добавления: 2015-07-21; просмотров: 46 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Ортогональность. | | | Эрмитовы операторы. |