Понятие оптимальной линейной фильтрации. Частотные характеристики оптимального линейного фильтра.

Пусть на линейный фильтр с комплексным коэффициентом передачи воздействует аддитивная смесь (сумма) сигнала и шума 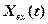. Если такую аддитивную смесь подать на линейный фильтр, то на выходе получается сумма шума и сигнала , действует принцип суперпозиции.

Пусть полностью известный сигнал

Шум 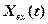– стационарный гауссовский СС в виде белого шума.

Введем понятие отношения сигнал-шум по напряжению на выходе цепи в момент времени .

(1)

Числитель – пиковое значение сигнала.

Линейный фильтр называется оптимальным, если при воздействии на него аддитивной смеси полностью известного сигнала и стационарного гауссовского белого шума получается наибольшее отношение сигнал-шум на выходе в момент времени (из всех возможных вариантов фильтров).

Это означает, что правилом оптимальности фильтров является критерий наибольшего отношения сигнал-шум на выходе фильтра.

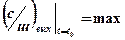
Определим какими частотными характеристиками должен обладать линейный фильтр, чтобы его можно было бы назвать оптимальным в указанном смысле.

Запишем

(2)

Воспользуемся для решения задачи оптимизации известным из математики неравенством Шварца-Буняковского

(3)

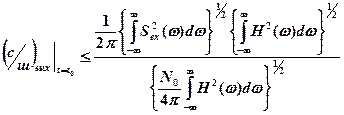(4)

Какими должны быть характеристики оптимального фильтра , , чтобы неравенство превратилось в равенство?

Сравним (2) и (4): для равенства их правых частей

или (5) – ФЧХ оптимального фильтра.

(6) – АЧХ оптимального фильтра.

– коэффициент пропорциональности.

Комплексный коэффициент передачи оптимального фильтра

(7),

* ─ знак комплексного сопряжения.

Подставим (5), (6), (7) в правую часть (4) и найдем отношение сигнал-шум на выходе оптимального фильтра:

(8)

Отношение сигнал-шум на выходе оптимального фильтра зависит только от энергии входного сигнала и спектральной плотности белого шума, то есть не зависит от формы сигнала. Объясняется это тем, что характеристики оптимального фильтра зависят от сигнала (согласованы с соответствующими характеристиками сигнала).

Благодаря последнему утверждению оптимальный линейный фильтр называют согласованным линейным фильтром.

Объясним, почему полученные характеристики (5) и (6) обеспечивают наибольшее отношение сигнал-шум на выходе фильтра в заданный момент времени t₀.

Начнем с выражения (5):

Согласно этому выражению в оптимальном фильтре происходит, во-первых, сдвиг всех гармонических составляющих сигнала s_вх(t) на время t₀. Во-вторых, в оптимальном фильтре происходит компенсация начальных фаз всех гармонических составляющих. В результате сдвига во времени и компенсации начальных фаз в момент времени t=t₀ все гармонические составляющие сигнала складываются своими амплитудными значениями, то есть образуется пик сигнала.

Рассмотрим выражение (6):

Из выражения (6) следует, что спектральные составляющие белого шума пропускаются оптимальным фильтром не равномерно, а с тем большим ослаблением, чем меньше значения спектральной характеристики сигнала на этой частоте. Это приводит к существенному ослаблению шума при прохождении оптимального фильтра.

Но такой вид АЧХ с другой стороны противоречит условию неискаженного прохождения сигнала через линейную цепь (АЧХ должна быть равномерной). В нашей задаче не ставится условие отсутствия искажения сигнала, так как форма сигнала заранее известна, а ставится условие получения максимального отношения сигнал-шум. Именно ценой искажения сигнала в оптимальном фильтре мы добиваемся максимального отношения сигнал-шум.

Одновременное выполнение условий (5) и (6) обеспечивает получение максимального отношения сигнал-шум на входе фильтра.

Дата добавления: 2015-07-20