Некоторые общие понятия теории графов.

Определение. Граф G^,′ (V′, E′) называется подграфом графа G(V, E), если V′ .

Обозначение: Таким образом, каждая вершина в G′ является вершиной в G, и каждое ребро в G′ ребром в G.

v₁ v₂

v₃ v₄

неограф без петель подграфы первого графа.

Путь (маршрут в графе) – это совокупность ребер, которые объединены вместе вершинами так, что вдоль них можно двигаться по графу.

Определение.

Пусть G=G(V, E) – граф с вершинами v₀, v_1, v₂,..., v_k, 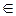V и ребрами e₁, e₂ e₃,..., e_k 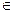E. Маршрутом на неориентированном графе G называется последовательность v₀, e₁, v ₁, e₂, v₂, e₃,..., v_{k -1}, e_k, v_k., где e_i = {v_{i – 1}, v_i}.

v₂

v₁ e₂ e₃

e₁ v₃

e₄

v₀ v₄

В дальнейшем маршрут будем обозначать через перечисление вершин.

Вершину v₀ называют началом, а v_k − концом пути.
Если v₀ = v_k, то маршрут называют циклом. Маршрут, в котором все ребра попарно различны, называют простым циклом (нет повторяющихся ребер). Цикл, в котором попарно различны все его вершины (кроме начальной и конечной вершины), называется элементарным циклом.

Связный граф называется эйлеровым, если нанем существует простой цикл, проходящий через все дуги графа (простой цикл, проходящий через все дуги графа, т.е. проходящий по одному разу через каждую дугу).

Теорема (критерий эйлеровости графа). Для того, чтобы конечный связный граф был эйлеровым. необходимо и достаточно, чтобы степени всех его вершин были четными числами.

Докажем необходимость. Она очевидна, т. к. в каждую вершину мы входим по одной дуге, а выходим по другой. Такая пара дуг дает вклад, равный двум в степень вершины. А, поскольку эйлеров цикл содержит все вершины, то сумма степеней будет четным числом.

Возвращаясь к вопросу о кенигсбергских мостах, следует отметить, что мультиграф, построенный Эйлером, имеет нечетные степени всех его вершин. Поэтому невозможно пройти каждый мост по одному разу и вернуться в исходную точку пути.

a

b c

d

Определение. Граф называется деревом, если он связен и не имеет циклов.

Определение. Несвязный неориентированный граф называется лесом.

Лес состоит из деревьев.

дерево лес.

---

Дата добавления: 2015-07-20