Двойной интеграл

Глава ХIII

1. Основные понятия. На плоскости Оху рассмотрим область S площади S, ограниченную замкнутой кривой g. Пусть в области S определена и непрерывна функция . Разобьем область S произвольным образом на n областей (рис. 3), имеющих площади и диаметры (диаметром области называется наибольшее из расстояний между двумя точками границы этой области). В каждой i –ой элементарной области выберем произвольную точку , значение функции в этой точке 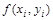умножим на площадь соответствующей области и все произведения сложим. Полученная сумма

называется интегральной суммой функции в области S.

Двойным интегралом от функции по области S называется конечный предел I интегральной суммы I_n при 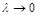, где .

.

y

y=j ₁(x)

y=j ₂(x)

О х О а b x

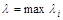Обозначения двойного интеграла:

.

Вычисление двойного интеграла сводится к вычислению повторных интегралов следующим способом. Пусть область S ограничена кривыми 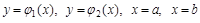(рис. 4), причем всюду на 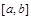функции и непрерывны и . Тогда

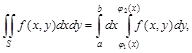(1)

причем сначала вычисляется внутренний интеграл по переменной у (х является параметром), а полученный результат интегрируется по х. Двойной интеграл, представленный в виде (1), называется повторным интегралом.

Если функция , интегрируемая в прямоугольнике , может быть представлена в виде произведения функции только от х на функцию только от у: , то

. (2)

Пример.

Вычислить интеграл , расставив пределы интегрирования двумя способами, где S – область, ограниченная линиями .

Решение.

Параболы, ограничивающие область S, пересекаются в двух точках (рис. 5).

1) Найдем пределы интегрирования:

, .

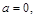
Запишем двойной интеграл в виде повторного по формуле (1):

2) Найдем пределы интегрирования:

.

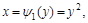
Запишем интеграл в виде (1):

Пример.

Вычислить интеграл , где область S является прямоугольником .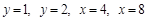

Решение.

Запишем данный интеграл в виде повторного:

.

Так как область S является прямоугольником, то по формуле (2) имеем

.

Дата добавления: 2015-07-20