Вычисление двойных интегралов

Рассмотрим для начала пример прямоугольной области R [ a, b; c, d ] (см. рис. 5). Покажем, что вычисление двойного интеграла сводится к вычислению повторного интеграла (двукратного).

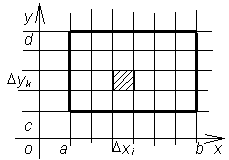
Рис. 5

Теорема 1. Если существует двойной интеграл 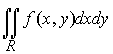и существует интеграл 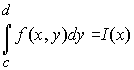при любых 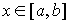и 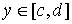, то существует и повторный интеграл, равный двойному

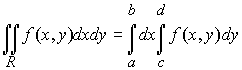. (7)

Не нарушая общности, докажем теорему для функции f (x, y), непрерывной в замкнутой области .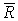

Доказательство. Разделим отрезок [ a, b ] точками

a = x ₀< x ₁< x ₂<...< x_n=b.

Через точки деления проведём прямые, параллельные оси оу:

x=x ₁, x=x ₂,..., x=x_n -1.

Отрезок [ c, d ] разделим точками на части и через эти точки проведём прямые, параллельные оси ох:

y=c, y=y ₁, y=y ₂,..., y=y_m -1.

Вся прямоугольная область R разделится на малые прямоугольники Rik (i = 1, 2, …, n; k = 1, 2, …, m).

Пусть m_ik - наименьшее значение, M_ik - наибольшее значение функции f (x, y) в R_ik, которые существуют по теореме Вейерштрасса для всякой функции, непрерывной в замкнутой области. Тогда для всех 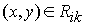выполняется неравенство

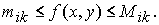
В частности, если 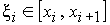, то

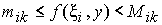
для всех .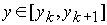

Проинтегрируем это неравенство по у от yk до yk +1:

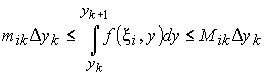. (8)

Просуммируем (8) по k, используя свойство аддитивности:

.

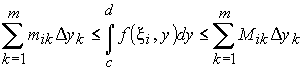Умножим все части неравенства на 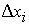и просуммируем по i:

.

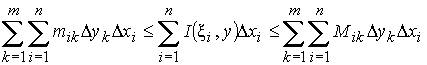Перейдём в последнем соотношении к пределу при :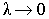

,

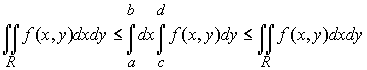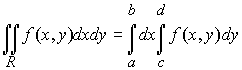. Теорема доказана.

Следует заметить, что в формулировке теоремы переменные х и у равноправны.

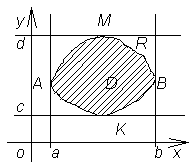
Рис. 6

Пусть теперь область D выпукла (см. рис. 6). Заключим нашу область в прямоугольник R со сторонами, параллельными осям координат. Граница области при этом точками касания разделится на две дуги. Пусть их уравнения будут таковы:
у = у ₁(х) - нижняя кривая (дуга АКВ),
у = у ₂(х) - верхняя кривая (дуга АМВ).

Теорема 2. Если существует интеграл

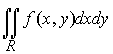
и существует интеграл

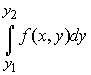при любом ,

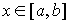то существует и повторный интеграл

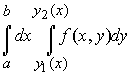
и он равен двойному интегралу

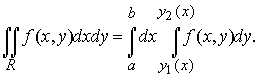(9)

Доказательство. Рассмотрим функцию

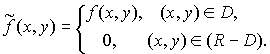
По теореме 1 можем записать

.

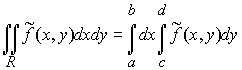Или, по свойству аддитивности, тот же интеграл можно представить как

.

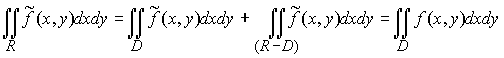Очевидно и другое равенство:

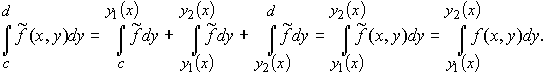
Объединяя все три равенства, получаем формулу

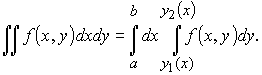
Теорема доказана.

Заметим, что существует ещё несколько доказательств теоремы 2 (вывода формулы 9). Приведём наиболее распространённое, опирающееся на геометрический смысл двойного интеграла как объёма цилиндрического тела (см. задачу 1), и задачу о вычислении объёма тела методом параллельных сечений с помощью определённого интеграла.

Пусть цилиндрическое тело, стоящее на плоскости хоу (см. рис. 7) ограничено сверху поверхностью z = f (x, y). Найдём его объём.

Построим сечениес помощью плоскости x = const, параллельной координатной плоскости yoz. Обозначим площадь этого сечения (криволинейной трапеции) S (x). Пусть проекция тела на плоскость хоу - правильная область D. Вынесем её чертёж отдельно (см. рис. 8) и заключим в прямоугольник R [ a, b, c, d ]. Точки касания А и В разобьют границу области на две кривые:

· АСВ с уравнением у = 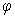₁(х),

· АЕВ с уравнением у = 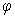₂(х).

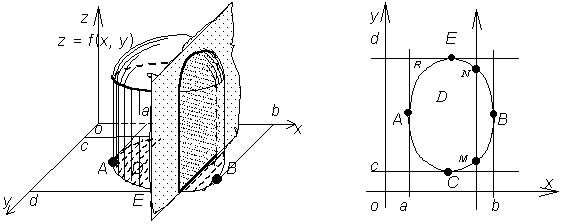
Рис. 7 Рис. 8

Будем считать функции 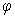₁(х) и 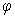₂(х) однозначными. При этом, как видно из рис. 8 и 7, точка М (назовём её точкой входа прямой x = const в область D) принадлежит линии у = 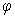₁(х), а точка N (назовём её точкой выхода) принадлежит линии у = 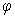₂(х).

Тогда площадь сечения S (x) можно выразить определённым интегралом

.

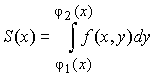Используя формулу вычисления объёма тела методом параллельных сечений

,

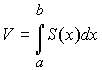запишем искомую формулу, представив двойной интеграл в виде двухкратного

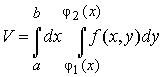, (10)

что и требовалось доказать.

Замечание 1. Можно было выполнить сечение тела плоскостью у = const, параллельной координатной плоскости хoz, и рассмотреть линии:

· САЕ с уравнением х = 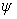₁(у),

· СВЕ с уравнением х = 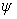₂(у).

В этом случае двойной интеграл записывается в виде другого двухкратного интеграла

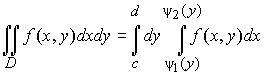. (11)

Замечание 2. Формулы (10) и (11) выражают сущность записи двухкратного интеграла:

· это число (в силу геометрического или физического смысла двойного интеграла), и, значит, пределы внешнего интеграла должны быть постоянны;

· пределы внутреннего интеграла в общем случае являются переменными, т. к. выражают (по последнему доказательству) площадь сечения тела для произвольного значения (хотя и фиксированного) одного из аргументов.

Замечание 3. При решении задачи о вычислении двойного интеграла немаловажную роль играет выбор порядка интегрирования в двухкратном интеграле. Если этот выбор неудачен, процесс интегрирования может сильно затянуться, а иногда привести к неберущимся интегралам.

Поэтому рекомендуем область интегрирования обязательно строить в системе координат, находя при этом точки пересечения граничных линий (если этих линий несколько).

Вычисление двухкратного интеграла начинаем с внутреннего интеграла (дифференциал указывает, по какой переменной надо интегрировать).

Замечание 3. При решении задачи о вычислении двойного интеграла немаловажную роль играет выбор порядка интегрирования в двухкратном интеграле. Если этот выбор неудачен, процесс интегрирования может сильно затянуться, а иногда привести к неберущимся интегралам.

Поэтому рекомендуем область интегрирования обязательно строить в системе координат, находя при этом точки пересечения граничных линий (если этих линий несколько).

Вычисление двухкратного интеграла начинаем с внутреннего интеграла (дифференциал указывает, по какой переменной надо интегрировать).

Дата добавления: 2015-07-20