Читайте также:
|
Вычет функции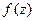 
в изолированной особой точке 
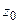определяется как коэффициент при 
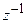в лорановском разложении 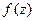с центром в :
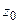(1) 
.
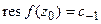Если 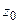— полюс первого порядка, можно использовать следующую формулу:
(2) 
.
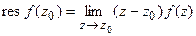Для полюса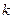 
-го порядка можно использовать следующую формулу:
(3) 
.
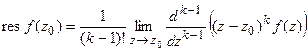TP 19.5. Найти вычеты функции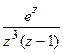 
в ее особых точках.
Решение: Здесь две особые точки: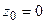 
— полюс третьего порядка и 
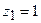— простой полюс. Для простого полюса используем формулу (2) и получаем
.
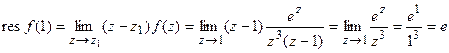Для полюса 3-го порядка используем формулу (3) и получаем
. ■
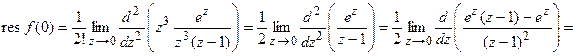
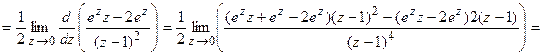
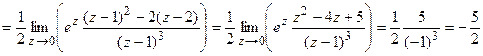TP 19.6. Найти вычеты функции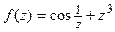 
в ее особых точках.
Решение: Здесь единственная особая точка 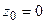. Раскладывая 
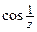в ряд Лорана в с центром в этой точки, получаем:
.
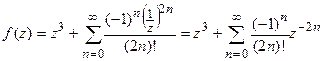Видим, что в лорановском разложении член с 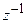отсутствует, и поэтому 
. ■
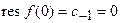TP 19.7. Найти вычеты функции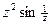 
в ее особых точках.
Решение: Здесь единственная особая точка 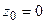. Раскладывая 
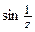в ряд Лорана в с центром в этой точки, получаем:
.
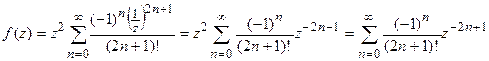Видим, что в лорановском разложении член с 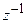соответствует 
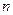, удовлетворяющему уравнению 
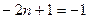, т.е. 
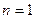, и поэтому 
. ■
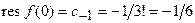TP 19.8. Найти вычеты функции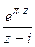 
в ее особых точках.
Решение: Здесь единственная особая точка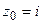 
— простой полюс. Применяем формулу (2):
. ■
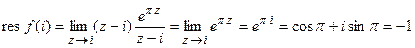Дата добавления: 2015-07-20; просмотров: 63 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Разложения функций в ряды Лорана | | | Вычисление интегралов при помощи вычетов |