Вычисление интегралов при помощи вычетов

Теорема (основная теорема о вычетах). Пусть функция 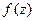аналитична в области 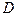за исключением конечного числа особых точек 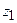, …, 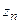. Пусть, далее, 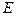— замкнутая область в 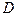, содержащая все особые точки внутри. Тогда имеет место формула:

(4) .

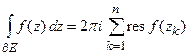TP 19.9. Вычислить интеграл .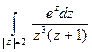

Решение: Особые точки: 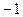— простой полюс и — полюс 3-го порядка — все попадают в круг 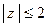. Вычисляем вычеты:

,

.

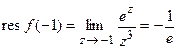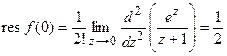По формуле (4) данный интеграл равен . ■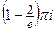

TP 19.10. Вычислить интеграл .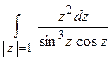

Решение: В круг 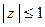попадает только — простой полюс.

.

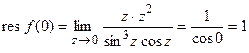По формуле (4) данный интеграл равен . ■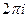

TP 19.11. Вычислить интеграл .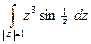

Решение: Здесь единственная особая точка 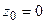— простой полюс. Раскладывая в ряд Лорана, видим, что 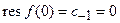и по формуле (4) данный интеграл равен нулю. ■

TP 19.12. Вычислить интеграл .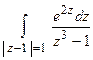

Решение: Единственная особая точка, входящая в круг 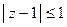— это точка 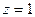0—0 простой полюс. Вычисляем вычет по формуле (2):

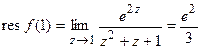. По формуле (4) искомый интеграл равен . ■

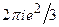ТР 19.13. Устранимая.

ТР 19.14. Существенно особая.

ТР 19.15. Устранимая.

ТР 19.16. Полюс 3-го порядка.

Дата добавления: 2015-07-20