|
Читайте также: |
ВЫЧЕТЫ
Точка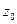 
называется нулем 
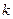-го порядка (кратности 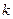) аналитической функции 
, если 
, но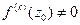 
, т.е. порядок нуля есть порядок младшей, отличной от нуля производной 
.
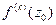Теорема. Для того, чтобы аналитическая в точке 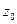функция имела в этой точке нуль 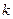-го порядка, необходимо и достаточно, чтобы в окрестности этой точки выполнялось равенство 
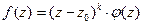, где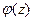 
- аналитическая в точке 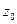функция, 
.
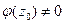Следствие. если многочлен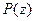 
имеет разложение 
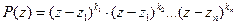, то точки 
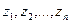- нули 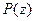кратностей 
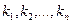соответственно.
Замечание. Если аналитична в своих нулях, то эти нули – точки, изолированные друг от друга.
Дата добавления: 2015-07-20; просмотров: 42 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Вычисление интегралов при помощи вычетов | | | Классификация изолированных особых точек |