Читайте также:
|
Пусть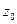 
- изолированная особая точка однозначной аналитической функции 
, т.е. в окрестности этой точки, ограниченной, например, контуром 
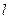, нет других особых точек. Разложим в окрестности этой точки функцию в ряд Лорана: 
.
Вычетом функции в конечной изолированной особой точке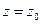 
(обозначается 
или 
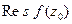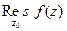, или 
, или 
называется коэффициент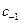 
при члене 
в разложении в ряд Лорана в окрестности точки .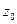
Если 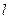- произвольный замкнутый контур, содержащий точку 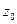внутри и лежащий в области аналитичности функции , то 
.
Основная Теорема о вычетах. Если функция аналитична в конечной замкнутой области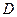 
, ограниченной контуром 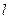, за исключением конечного числа особых точек 
, лежащих внутри области 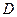, то 
, т.е. интеграл от функции по контуру 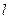в положительном направлении равен произведению 
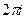на сумму вычетов во всех точках 
.
Дата добавления: 2015-07-20; просмотров: 41 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Классификация изолированных особых точек | | | Пусть - устранимая особая точка, т.е. ряд Лоран в кольце не содержит главной части. |