
|
Читайте также: |
Пусть область 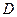 ограничена кривой
ограничена кривой 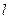 , состоящей из двух лучей
, состоящей из двух лучей  и
и  , выходящих из точки
, выходящих из точки 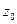 и определяемых уравнениями
и определяемых уравнениями  и
и 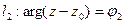 .
.
Пусть  аналитична в области
аналитична в области 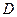 и непрерывна на ее границе
и непрерывна на ее границе 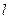 , за возможным исключением конечного числа точек
, за возможным исключением конечного числа точек  . Обозначим
. Обозначим 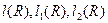 те части кривых
те части кривых  соответственно, которые лежат в круге
соответственно, которые лежат в круге 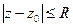 .
.
Интеграломпо неограниченной кривой 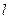 от функции
от функции  называется сумма пределов
называется сумма пределов  .
.
Направление на кривой 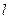 выбирают так, чтобы область
выбирают так, чтобы область 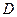 при обходе оставалась слева.
при обходе оставалась слева.
Главным значением интеграла по кривой 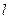 называют предел
называют предел  ,
,  .
.
Замечание. Если кривая 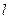 совпадает с действительной осью (
совпадает с действительной осью ( ), получается обычное определение несобственного интеграла
), получается обычное определение несобственного интеграла  . Если же
. Если же 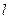 совпадает с вертикальной прямой
совпадает с вертикальной прямой  , то главное значение интеграла
, то главное значение интеграла  .
.
На случай рассмотренной области 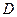 основная теорема о вычетах распространяется следующим образом:
основная теорема о вычетах распространяется следующим образом:
Теорема 6. Если функция  аналитична в области
аналитична в области 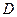 и непрерывна на ее границе
и непрерывна на ее границе 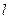 , за исключением конечного числа особых точек
, за исключением конечного числа особых точек  , и если
, и если  , то
, то  . Здесь
. Здесь  - та часть окружности
- та часть окружности  , которая лежит в области
, которая лежит в области 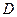 .
.
С помощью этой теоремы можно распространить на неограниченный контур 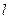 интегральную формулу Коши.
интегральную формулу Коши.
Теорема 7. Если функция  аналитична в области
аналитична в области 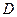 и непрерывна на ее границе
и непрерывна на ее границе 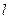 , и если
, и если  , то для любой точки
, то для любой точки 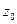 области
области 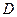
 .
.
Из теоремы 6 можно получить еще одну удобную для вычисления несобственных интегралов формулу:
Теорема 8. Если рациональная функция  не имеет полюсов на вещественной оси и степень знаменателя
не имеет полюсов на вещественной оси и степень знаменателя  , по крайней мере, на две единицы выше степени числителя
, по крайней мере, на две единицы выше степени числителя 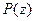 , то
, то 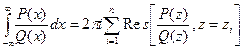 , где
, где  - нули функции
- нули функции  , лежащие в верхней полуплоскости.
, лежащие в верхней полуплоскости.
Дата добавления: 2015-07-20; просмотров: 36 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Вычисление интегралов с помощью вычетов | | | Страхование в международной торговой практике |