Пусть - устранимая особая точка, т.е. ряд Лоран в кольце не содержит главной части.

Теорема 1. Вычет в устранимой особой точке равен нулю.

2. Пусть 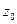- простой полюс функции , т.е. полюс первого порядка.

а) ряд Лорана функции имеет вид

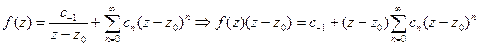. Поэтому

.

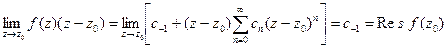Теорема 2. Если точка 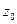- простой полюс , то .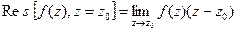

б) другой способ вычисления вычета в полюсе первого порядка. Если 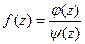и точка 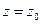является простым нулем функции 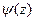, а 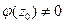, то точка 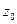будет простым полюсом функции .

Теорема 3. Если 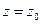- простой полюс функции 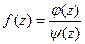, то .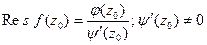

3. Пусть 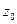- полюс кратности .

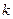Теорема 4. Если точка 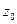- полюс функции порядка 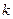, то

.

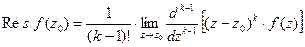4. Пусть 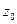- существенно особая точка, т.е. главная часть Лорана в окрестности точки 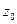содержит бесконечное число слагаемых. Чтобы найти вычет в существенно особой точке. нужно

а) либо найти коэффициент 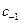в разложении функции в ряд Лорана ,

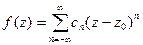б) либо вычислить .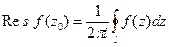

5. Вычетом функции в точке 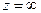называется коэффициент при члене 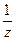в разложении в ряд Лорана в окрестности точки 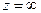, взятый с обратным знаком, т.е. .

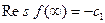Ряд Лорана для функции в окрестности точки 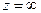: . При такой замене правильная часть ряда заменяется главной и обратно.

Теорема 5. Если функция аналитична на расширенной плоскости, за исключением конечного числа особых точек, то сумма всех ее вычетов (включая и вычет в точке 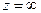) равна нулю, т.е. .

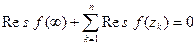Дата добавления: 2015-07-20