
Читайте также:
|
В особых точках функции  нарушается ее аналитичность.
нарушается ее аналитичность.
Изолированные особые то чки – особые точки простейшего типа.
Точка 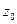 называется изолированной особой точкой функции
называется изолированной особой точкой функции  , если существует такая ее окрестность, во всех точках которой
, если существует такая ее окрестность, во всех точках которой  аналитична, за исключением самой точки
аналитична, за исключением самой точки 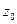 . Если
. Если 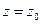 - изолированная особая точка
- изолированная особая точка  , то существует такое достаточно малое кольцо
, то существует такое достаточно малое кольцо  , в котором функция
, в котором функция  аналитична и в котором, следовательно,
аналитична и в котором, следовательно,  разлагается в ряд Лорана:
разлагается в ряд Лорана:
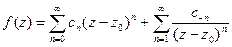 .
.
При этом возможны три случая:
1. Главная часть ряда Лорана отсутствует:
 . В этом случае особая точка
. В этом случае особая точка 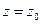 называется устранимой.
называется устранимой.
2. Главная часть имеет конечное число членов:
 , где
, где  . В этом случае точка
. В этом случае точка 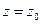 называется полюсом
называется полюсом 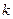 -го порядка. Если
-го порядка. Если  , полюс называется простым, в остальных случаях – кратным.
, полюс называется простым, в остальных случаях – кратным.
3. Главная часть имеет бесконечное число слагаемых 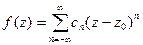 , тогда точка
, тогда точка 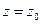 называется существенно особой точкой.
называется существенно особой точкой.
Теорема 1. Для того, чтобы 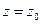 была устранимой особой точкой функции
была устранимой особой точкой функции  , необходимо и достаточно, чтобы существовал конечный предел
, необходимо и достаточно, чтобы существовал конечный предел  .
.
Если  , то
, то 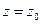 называется полюсом.
называется полюсом.
Замечание. Если  , где
, где 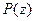 и
и  - полиномы, не имеющие общих корней, то корни полинома
- полиномы, не имеющие общих корней, то корни полинома  (и только они) являются полюсами функции
(и только они) являются полюсами функции  .
.
Теорема 2. Для того, чтобы 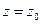 была полюсом
была полюсом 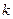 -го порядка функции
-го порядка функции  , необходимо и достаточно, чтобы в некоторой окрестности точки
, необходимо и достаточно, чтобы в некоторой окрестности точки 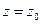 имело место равенство
имело место равенство  , где
, где 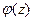 - аналитическая в окрестности точки
- аналитическая в окрестности точки 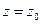 функция.
функция.
Если 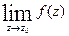 не существует, то
не существует, то 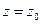 называется существенно особой точкой.
называется существенно особой точкой.
Замечание. Если функция  имеет в точке
имеет в точке 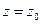 нуль
нуль 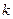 -го порядка, то функция
-го порядка, то функция  имеет в этой точке полюс того же порядка.
имеет в этой точке полюс того же порядка. 

Дата добавления: 2015-07-20; просмотров: 53 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Нули аналитических функций | | | Понятие вычета |