Свойства двойного интеграла

Перечислим свойства двойного интеграла, не доказывая их, т. к. они полностью идентичны свойствам определённого интеграла.

1. Если функция интегрируема в области D, то функция сf (x, y), где c = const, тоже интегрируема в области D и

.

Иначе: константу можно выносить за знак интеграла.

2. Если функции f (x, y) и 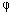(x, y) интегрируемы в области D, то функция f (x, y) + 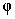(x, y) тоже интегрируема в области D и

.

3. Если f (x, y) = 1 для всех точек области D, то

,

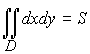где S - площадь области D.

4. Если , то и

.

5. Если для двух функций, интегрируемых в области D, выполняется неравенство

,

то

.

6. Еслифункция f (x, y)интегрируема, тофункция | f (x, y)| также интегрируема в области D и

,

при этом функция f (x, y) называется абсолютно интегрируемой в D.

7. Если область интегрирования D разбить прямой, параллельной одной из координатных осей, на две непересекающиеся области D ₁ и D ₂, например, как указано на рис. 4, то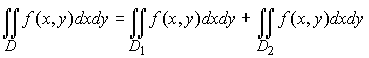

Рис. 4

Вышеуказанная формула демонстрирует свойство аддитивности двойного интеграла. Свойство можно распространить на любое конечное число делений области D.

8. Теорема об оценке двойного интеграла. Если функция f (x, y) задана в замкнутой области D (обозначим 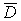) и т, М соответственно её наименьшее и наибольшее значения в этой области, а S - площадь области D, то

.

9. Теорема о среднем значении функции f (x, y). Если функция f (x, y) непрерывна в области 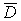, то найдётся точка 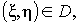такая, что

или

.

Геометрический смысл этой теоремы таков: объём цилиндрического тела равен объёму цилиндра с тем же основанием и высотой, равной значению функции в точке .

---

Дата добавления: 2015-07-20