Исследование явления двойного лучепреломления, построение волновых поверхностей

Лабораторная работа № 12

Цель работы: Построение волновой поверхности одноосного кристалла.

Оборудование: 1. Лазер-указка «DANGER» или ЛГН–109.

1. Исследуемый кристалл исландского шпата.

2. Столик со шкалой, позволяющий изменять углы падения луча на кристалл.

3. Анализатор с угловой шкалой.

4. Полоски тонкой бумаги.

5. Экран.

6. Маркер.

7. Кювета с водой.

8. Транспортир.

ТЕОРИЯ

В изотропных телах электрические, а, следовательно, и оптические свойства вещества одинаковы по всем направлениям. К изотропным телам относятся газы, большинство жидкостей, аморфные твердые тела и высокосимметричные кристаллы. В низкосимметричных кристаллах наблюдается различие электрических и оптических свойств для различных направлений. Электрические свойства несимметричных кристаллов для различных направлений электрического поля оказываются различными. Вещества, у которых электрические и оптические свойства зависят от направления, называются анизотропными.

Основное оптическое явление, которое имеет место при распространении света в кристаллах, - это двойное лучепреломление, т.е. раздвоение вошедшего в кристалл светового луча при его преломлении.

Для изотропных веществ между вектором электрической индукции и вектором напряженности электрического поля Е существует связь:

,

где e - диэлектрическая проницаемость среды. Соответственно, компоненты вектора D по осям координат x, y, z запишутся в виде:

D_x = e₀eE_x; D_y = e₀eE_y; D_z = e₀eE_z,

откуда видно, что диэлектрическая проницаемость среды по всем направлениям одинакова, а из закона Максвелла следует, что и скорость распространения света по всем направлениям в такой среде постоянна, .

Для анизотропных веществ (низкосимметричных кристаллов) связь между D и E более сложная. Если в качестве осей координат выбрать главные электрические оси кристалла, то связь между проекциями D и Е может быть записана в более простом виде:

D_x = e₀e_хE_x;

D_y = e₀e_yE_y;

D_z = e₀e_zEz,

где e_х, e_y, e_z - значения диэлектрической проницаемости соответственно для случаев действия электрического поля по выбранным осям x,y,z. Следовательно, показатель преломления среды по разным направлениям различен, а значит, различна и скорость света в такой среде по разным направлениям.

Еще в 1670 г. Бартолинус наблюдал, что при прохождении через исландский шпат (СаCО₃) световой луч разделяется на два. По выходе из кристалла оба луча имеют направления, параллельные первоначальному, и, если световые пучки достаточно узкие, а кристалл достаточно толст, то они пространственно разделены (рис. 1).

Рис. 1

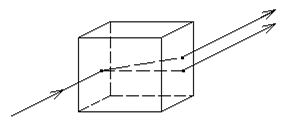При рассмотрении какого-либо объекта глазом через такой кристалл - объект двоится.

Исследование направлений обоих лучей, возникающих внутри кристалла, показало, что для одного из лучей отношение

,

где a - угол падения, а b - угол преломления, т.е. остается постоянным при изменении угла падения.

Этот луч лежит в одной плоскости с падающим лучом и нормалью к поверхности кристалла в точке падения, таким образом, этот луч удовлетворяет обычному закону преломления и потому называется обыкновенным.

Второй луч называется необыкновенным. Для него отношение

,

т.е., не остается постоянным при изменении угла падения. Необыкновенный луч, как правило, не лежит в одной плоскости с падающим лучом и нормалью к преломляющей поверхности. По выходе же из кристалла необыкновенный луч снова подчиняется законам геометрической оптики, сохраняя лишь прежнее направление колебания вектора Е. Оба луча полностью поляризованы и колебания векторов Е_о и Е_е в них происходят во взаимно перпендикулярных плоскостях.

В кристаллах существуют направления, при прохождении света вдоль которых не образуется двух лучей. Прямая, проведенная через любую точку кристалла в направлении, в котором не происходит двойного лучепреломления, называется оптической осью. Плоскость, содержащая оптическую ось и луч, называется главным сечением или главной плоскостью кристалла. Через одноосный кристалл, очевидно, можно провести бесчисленное множество оптических осей и бесконечное множество главных плоскостей.

Кристаллы, имеющие лишь одно направление, вдоль которого не происходит двойное лучепреломление, называются одноосными. В большинстве прозрачных одноосных кристаллах яркость обыкновенного и необыкновенного лучей одинакова. Однако существуют кристаллы, в которых один из лучей поглощается сильнее другого. Такое различное поглощение называется дихроизмом. Весьма сильным дихроизмом в видимом свете обладает кристалл турмалина, который при толщине в 1 мм практически полностью поглощает обыкновенный луч. Аморфные тела при деформациях и жидкости в электрическом поле (Эффект Керра) приобретают свойства двойного лучепреломления.

Объяснение явлению двойного лучепреломления в одноосных кристаллах впервые дано Гюйгенсом в 1690 году. Он предположил, что обыкновенному лучу соответствует возникновение в кристалле волновой поверхности в виде сферы, а необыкновенному - в виде эллипсоида вращения. Гипотеза Гюйгенса соответствует современным представлениям о природе света и строении кристаллов.

Атомы, ионы или молекулы, из которых построены кристаллы, являются анизотропными вибраторами. Это означает, что колебания в них совершаются в различных направлениях с различными собственными частотами.

Пусть частицы, из которых построен кристалл, обладают собственной частотой колебания w₁ при колебаниях вдоль направления, параллельного оптической оси кристалла, и собственной частотой колебания w₂ - при колебаниях, перпендикулярных к оптической оси. Колебаниям, совершающимся

в каких-либо других направлениях по отношению к оптической оси, соответствуют собственные частоты w, промежуточные между w₁ и w₂.

Пусть направление оси кристалла параллельно стороне АВ. Точечный источник S посылает поляризованные лучи во все стороны (рис. 2).

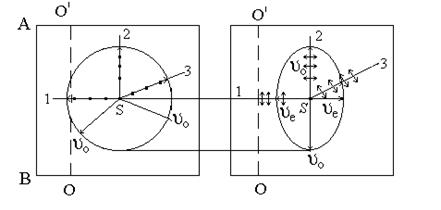а б

Рис. 2

Как видно из рис. 2, а колебания вектора Е перпендикулярны к оптической оси для любого из лучей 1, 2, 3, Благодаря этому световая волна раскачивает вибраторы лишь в направлениях, перпендикулярных к оптической оси, которым соответствует одна и та же частота собственных колебаний w₂, следовательно, e по всем направлениям постоянна, а , , т.е. световые волны распространяются по всем направлениям с одинаковой скоростью υ_о. Геометрическим местом точек, до которых лучи, исходящие из S, будут доходить за одинаковый промежуток времени, будет сфера.

Рассмотрим лучи, в которых колебания электрического вектора совершаются в плоскости главного сечения кристалла (т.е. в плоскости чертежа). Как видно из рис. 2 б, для различных лучей 1, 2, 3, колебания вектора Е направлены под различными углами к оптической оси. Колебание вектора Е_е в луче 2 вызывает колебания вибраторов с собственной частотой w₂, и, следовательно, распространяется со скоростью υ_о, луч 1 вызывает колебания вибраторов с собственной частотой w₁, следовательно, и скорость распространения у него должна быть иная, чем у луча 2, обозначим ее через υ_е. Луч 3 будет распространяться со скоростью υ¢, промежуточной между υ_о и υ_е. В результате этого волновая поверхность будет иметь вид эллипсоида вращения. Лучи, соответствующие такой волновой поверхности, не подчиняются обычному закону преломления и носят название необыкновенных.

Кристаллы, у которых υ_е< υ_о, т.е. n_е > n_о, называются положительными (рис. 3 а).

Кристаллы, у которых υ_е> υ_о, т.е. n_е < n_о, называются отрицательными. (рис. 3 б).

а б

Рис. 3

В обоих случаях оптическая ось ОО¢ проходит через точки соприкосновения эллипсоидальной и сферической поверхностей – вдоль ее скорости распространения лучей, поляризованных в любой плоскости, одинаковы.

Для нахождения направлений распространения лучей обыкновенных и необыкновенных в одноосных кристаллах используем представление о сферической и эллипсоидальной волновых поверхностях для ряда частных случаев.

I. Оптическая ось кристалла ОО¢ параллельна преломляющей грани ММ,
на которую падает плоский фронт волны АВ (рис. 4).

Около точек А и В возникнут по две волновых поверхности - сферическая и эллипсоидальная, соприкасающиеся друг с другом в направлении оптической оси ОО¢

По принципу Гюйгенса необходимо провести две поверхности: C¢D¢ - касательную к сферам, и Е¢F¢ - касательную к эллипсоидам. Первая дает фронт преломленной обыкновенной волны, вторая - фронт преломленной необыкновенной волны.

Рис. 4

Соединив точки А с С и В с D, получим направление обыкновенных лучей; если соединить точки А с Е и В с F, где Е и F точки касания эллиптических поверхностей с плоскостью E¢ F¢, получим направление необыкновенных лучей. В этом случае обыкновенные и необыкновенные лучи идут не преломившись, и распространяются в кристалле в одном и том же направлении. Однако, фронты C¢ D¢ и E¢ F¢ обыкновенной и необыкновенной волн не совпадают. В случае отрицательного кристалла фронт необыкновенной волны обгонит фронт обыкновенной, в результате между обыкновенными и необыкновенными волнами возникает определенная разность хода. При этом нужно помнить, что колебания векторов Е_е и Е₀ происходит во взаимно перпендикулярных плоскостях. После выхода из кристалла произойдет сложение этих взаимно перпендикулярных колебаний, результат которого зависит от приобретенной разности хода.

II. Оптическая ось перпендикулярна преломляющей грани ММ, на которую падает плоский фронт волны АВ.

Свет падает нормально на преломляющую грань и, следовательно, параллельно оптической оси (рис. 5).

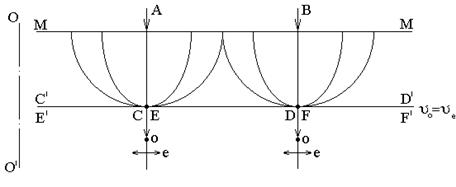Рис. 5

Около каждой из точек А и В возникнут по две волновые поверхности - сферическая и эллипсоидальная. Проведенные касательные С¢D¢ и E¢F¢ совпадают, следовательно, внутри кристалла, по одному направлению распространяются обыкновенная и необыкновенная волны с одинаковой скоростью, но с взаимно перпендикулярными направлениями колебаний векторов Е₀ и Е_е. Разности хода между волнами не возникают, поэтому после выхода из кристалла состояние поляризации падающего света не изменится.

III. Оптическая ось кристалла ОО¢ лежит в плоскости падения, образуя угол a с преломляющей поверхностью, а лучи падают на границу раздела нормально. (рис. 6).

C¢D¢ - фронт обыкновенной волны, точки касания С и D. E¢F¢ - фронт необыкновенной волны, точки касания E и F.

Обыкновенная волна распространяется по направлениям АС и ВD; необыкновенная - АЕ и ВF, из кристалла выйдут два пространственно разделенных луча, поляризованных взаимно перпендикулярно.

Рис. 6

МЕТОДИКА ВЫПОЛНЕНИЯ РАБОТЫ

I. Исследование явления двойного лучепреломления.

Соберите установку, изображенную на рис. 7, где 1– лазер,2– кристалл, 3 – анализатор, 4 –экран.

Рис. 7

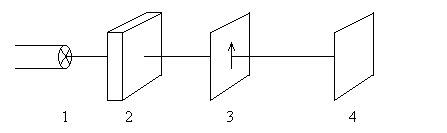1. Включите лазер. Луч света, проходя через кристалл, испытывает явление двойного лучепреломления. На экране наблюдаются два световых пятна.

2. Начните вращать анализатор, добиваясь гашения одного из лучей. Запишите в табл.1 на какой угол a для достижения этого эффекта пришлось повернуть анализатор.

3. Продолжайте вращать анализатор. Сначала возникнет первоначально погашенный луч, затем произойдет гашение второго луча. Впишите в табл.1 угол b на каторый нужно повернуть анализатор, чтобы погасить второй луч.

4. Повторите опыт 3 раза.

5. Из табл.1 сделайте вывод о характере и о направлении поляризации лучей относительно друг друга.

Таблица 1

№
a
b

II. Построение волновой поверхности необыкновенных лучей для одноосного кристалла исландского шпата.

Идея метода заключается в нахождении показателя преломления n_е необыкновенного луча при разных углах падения луча на кристалл.

Для этого соберите установку (рис. 8), где: 1 – лазер, 2 –предметный столик со шкалой, на котором закреплен кристалл.

Рис. 8

На рис. 9 показан ход лучей внутри кристалла, где: 1 – лазер,

2 – столик со шкалой, 3– кристалл исландского шпата.

Кристалл закреплен так, что входная грань NN¢ M¢M строго вертикальна и начало отсчета на шкале совпадает с перпендикуляром АВ к исследуемому кристаллу.

Из рис. 9 видно, что:

АВ -^ к грани кристалла КLL¢К¢;

SA - направление луча, падающего на кристалл;

a - угол падения;

АС₀ - направление преломленного обыкновенного луча;

АС¢_е- направление необыкновенного луча;

Ð ВАС₀ = b₁ где b₁ - угол преломления обыкновенного луча;

Ð ВАС¢_е = b₂ где b₂ - угол преломления необыкновенного луча;

d - толщина кристалла (ML);

h - расстояние между точками выхода лучей (С₀С¢_е).

Рис. 9

Из закона преломления имеем:

. (1)

Из треугольника АВС х = d tgb₁, где х = ВС₀. (2)

Из треугольника АВС¢ ,

С₀С¢_е = h, C¢_еB = h + x, . (3)

Показатель преломления необыкновенного луча равен:

. (4)

1. С помощью штангенциркуля измерьте толщину кристалла d три раза, d_ср запишите над таблицей 2.

2. Включите лазер, установите кристалл таким образом, чтобы луч падал перпендикулярно грани NMM¢N¢, ближе к левой стороне.

3. Смочите полоску бумаги (кальки) в воде и приложите ее к грани кристалла KLL¢K¢.

4. Медленно вращая кристалл на предметном столике, изменяйте угол падения луча a, начиная с 20° через 10° до 80°. При этом на бумаге, прикрепленной к грани кристалла, отмечайте маркером положение светящихся точек, перемещая каждый раз полоску бумаги вдоль грани KLL¢K¢

5. Cнимите бумагу и с помощью штангенциркуля определите величину - h.

6. Используя выражения (2) и (3), вычислите углы преломления необыкновенного луча.

7. По формуле (4) найдите показатель преломления необыкновенного луча для разных углов падения.

8. По полученным результатам постройте зависимость n_e = f (a) для необыкновенного луча (рис. 10). Для чего от точки О откладывайте семь радиусов, которые задаются углом a и длиной, равной рассчитанной величине n_e.

Результаты измерений внесите в табл.2.

Рис. 10

d_ср =

Таблица 2

a	Sinβ1/ β1	tgb1	x	h	tgb2/β2	Sinb2	ne

В этом случае Вы получаете ¼ часть эллипса. Симметрично этому построению постройте 3 оставшиеся части эллипса. Полученный эллипс - след сечения эллипсоидальной поверхности плоскостью рисунка.

Поверхность показателя преломления для обыкновенного луча в исландском шпате - сфера, имеющая радиус, равный n_o = 1,66.

Используя формулу

, (5)

вычислите скорости необыкновенного луча по разным направлениям. Результаты вычислений внесите в табл.2. Постройте волновые поверхности обыкновенного и необыкновенного лучей

Контрольные вопросы

1. Какой свет называется естественным?

2. Какой свет называется линейно – поляризованным?

3. Каким образом можно отличить естественный свет от линейно – поляризованного?

4. Какие вещества называются изотропными? Анизотропными? Их свойства?

5. В каких средах возникает явление двойного лучепреломления?

6. Какой луч называется обыкновенным? Необыкновенным? Какими свойствами обладают эти лучи?

7. Что называется оптической осью кристалла? Как ведет себя световая волна, распространяясь вдоль оси?

8. Какие плоскости в кристалле называются главными? Сколько их в одноосном кристалле?

9. Объяснить физическую природу возникновения волновых поверхностей (сферической и эллипсоидальной) в анизотропных веществах.

10. Объяснить направление распространения лучей обыкновенного n₀ и необыкновенного n_e в кристальных средах, для различных случаях расположения оси кристалла.

11. Какие кристаллы называются положительными? Отрицательными?

12. Знать вывод рабочей формулы (4).

Библиографический список

1. Ландсберг Г.С. Оптика. М.; Наука, 1976 г.

2. Королев Ф.А. Курс физики. Оптика, физика атома и атомного ядра. М.; Просвещение, 1974.

3. Фриш С.Э. и Тиморева А.В. Курс общей физики. Т.Ш, 1961.

4. Гершензон Е.М. и др. "Курс общей физики. М.; Просвещение, 1981.

5. Калитиевский Н.И. Волновая оптика. Учебное пособие для ВУЗов. М.; Высшая школа, 1995.

6. Трофимова Т.И. Курс физики. Учебное пособие. М.; Высшая школа, 1998.

Дата добавления: 2015-07-20