Замена переменных в двойном интеграле.

Если непрерывно дифференцируемые функции осуществляют взаимно однозначное отображение области S плоскости Oxy на плоскость G плоскости Ouv, то

, (4)

где – функциональный определитель (якобиан):

.

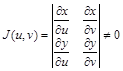В случае перехода к полярным координатам , формула (4) принимает вид:

.

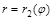
Если область G ограничена лучами, образующими с полярной осью углы , и кривыми и , то

.

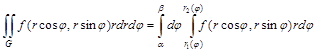Пример.

х

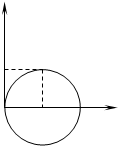
Перейдя к полярным координатам, вычислить двойной интеграл 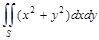, где область S ограничена окружностью 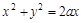(рис. 7).

Решение.

а

Так как , то

.

Уравнение окружности преобразуется к виду . Поэтому область G – это область, ограниченная снизу осью 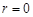, сверху синусоидой , причем .

Следовательно,

Дата добавления: 2015-07-20