
Читайте также:
|
16.1.4.1. Определение простой (правильной) области. Область  на плоскости Oxy будем называть простой (правильной) в направлении оси Oy, если любая прямая, проходящая через внутреннюю точку области
на плоскости Oxy будем называть простой (правильной) в направлении оси Oy, если любая прямая, проходящая через внутреннюю точку области  и параллельная оси Oy, пересекает границу
и параллельная оси Oy, пересекает границу  в двух точках.
в двух точках.
Аналогично определяется область, простая (правильная) в направлении оси Ox: любая прямая, проходящая через внутреннюю точку области  и параллельная оси Oх, пересекает границу
и параллельная оси Oх, пересекает границу  в двух точках.
в двух точках.
Область, правильную (простую) в направлении обеих осей, будем называть правильной.

 |
 , правильную в направлении оси Oy, можно описать неравенствами
, правильную в направлении оси Oy, можно описать неравенствами  . Числа
. Числа  и
и  существуют вследствие ограниченности области
существуют вследствие ограниченности области  , функция
, функция  образована нижними точками пересечения прямой
образована нижними точками пересечения прямой  при
при  с границей области
с границей области  , функция
, функция  - верхними точками пересечения этой прямой с границей области
- верхними точками пересечения этой прямой с границей области  :
:
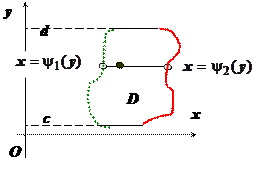
Аналогичным образом область  , ограниченную, замкнутую и правильную в направлении оси Oх, можно описать неравенствами
, ограниченную, замкнутую и правильную в направлении оси Oх, можно описать неравенствами  . Функция
. Функция 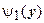 образована левыми точками пересечения прямой
образована левыми точками пересечения прямой  при
при  с границей области
с границей области  , функция
, функция  - правыми точками пересечения этой прямой с границей области
- правыми точками пересечения этой прямой с границей области  .
.
 Для правильной области (т.е. области, правильной в направлении обеих осей) существуют оба способа представления: и
Для правильной области (т.е. области, правильной в направлении обеих осей) существуют оба способа представления: и  , и
, и  .
.
16.1.4.2. Двукратный (повторный) интеграл. Пусть  - область, простая в направлении оси Oy. Рассмотрим выражение
- область, простая в направлении оси Oy. Рассмотрим выражение  . Эта конструкция определяется через два обычных определённых интеграла. После интегрирования по у во внутреннем интеграле (переменная х при этом рассматривается как постоянная) и подстановки по у в пределах от
. Эта конструкция определяется через два обычных определённых интеграла. После интегрирования по у во внутреннем интеграле (переменная х при этом рассматривается как постоянная) и подстановки по у в пределах от  до
до  получается функция, зависящая только от х, которая интегрируется в пределах от a до b. В дальнейшем мы будем обычно записывать этот объект без внутренних скобок:
получается функция, зависящая только от х, которая интегрируется в пределах от a до b. В дальнейшем мы будем обычно записывать этот объект без внутренних скобок:
 .
.
Можно показать, что двукратный интеграл обладает всеми свойствами двойного интеграла:
Свойства линейности и интегрирования неравенств следуют из этих свойств определённого интеграла; интеграл от единичной функции даёт площадь области  :
:  ;
;
 теоремы об оценке и о среднем следуют из перечисленных свойств. Единственное свойство, с которым придётся повозиться - это свойство аддитивности. Мы докажем его в простой, но достаточной для нас форме: если область
теоремы об оценке и о среднем следуют из перечисленных свойств. Единственное свойство, с которым придётся повозиться - это свойство аддитивности. Мы докажем его в простой, но достаточной для нас форме: если область  разбита на две подобласти
разбита на две подобласти  и
и  прямой, параллельной одной из координатных осей, то двукратный интеграл по области
прямой, параллельной одной из координатных осей, то двукратный интеграл по области  равен сумме интегралов по
равен сумме интегралов по  и
и  :
: 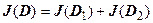 .
.
 Первый случай: прямая
Первый случай: прямая  параллельна оси Oy. Тогда
параллельна оси Oy. Тогда  (аддитивность внешнего интеграла)
(аддитивность внешнего интеграла)  .
.
Второй случай: прямая  параллельна оси Oх. Воспользуемся сначала аддитивностью внешнего интеграла:
параллельна оси Oх. Воспользуемся сначала аддитивностью внешнего интеграла: 
|
 (теперь применим свойство аддитивности для внутреннего интеграла в среднем слагаемом) =
(теперь применим свойство аддитивности для внутреннего интеграла в среднем слагаемом) =  (применяем свойство линейности для внешнего интеграла в среднем слагаемом и перегруппировываем сумму)=
(применяем свойство линейности для внешнего интеграла в среднем слагаемом и перегруппировываем сумму)= 

(первая фигурная скобка даёт повторный интеграл по  , второй - по
, второй - по  )
)  .
.
 Понятно, что воэможны различные случаи взаимного расположения прямых
Понятно, что воэможны различные случаи взаимного расположения прямых  ,
,  ,
,  и функций
и функций  ,
,  , но логика доказательства во всех случаях такая же.
, но логика доказательства во всех случаях такая же.
Обобщим доказанное свойство. Пусть прямая разбивает область  на две подобласти
на две подобласти  и
и 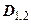 . Проведём ещё одну прямую, параллельную какой-либо координатной оси. Пусть эта прямая разбивает
. Проведём ещё одну прямую, параллельную какой-либо координатной оси. Пусть эта прямая разбивает  на
на  и
и  ;
; 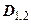 - на
- на 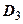 и
и  . По доказанному,
. По доказанному,  ,
, 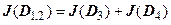 , поэтому
, поэтому  . Продолжая рассуждать также, убеждаемся в справедливости следующего утверждения: если область
. Продолжая рассуждать также, убеждаемся в справедливости следующего утверждения: если область  с помощью прямых, параллельных координатным осям, разбита на подобласти
с помощью прямых, параллельных координатным осям, разбита на подобласти  , то
, то  .
.
16.1.4.3. Теорема о переходе от двойного интеграла к повторному. Пусть  - простая в направлении оси Oy область. Тогда двойной интеграл от непрерывной функции по области
- простая в направлении оси Oy область. Тогда двойной интеграл от непрерывной функции по области  равна повторному интегралу от той же функции по области
равна повторному интегралу от той же функции по области  :
:  .
.
Док-во. Разобьём область  с помощью прямых, параллельных координатным осям, на подобласти
с помощью прямых, параллельных координатным осям, на подобласти  . По доказанному выше,
. По доказанному выше, 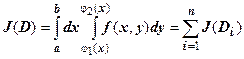 . К каждому из итегралов
. К каждому из итегралов  применим теорему о среднем: в любой области
применим теорему о среднем: в любой области 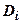 найдётся точка
найдётся точка 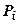 такая, что
такая, что  . Следовательно,
. Следовательно,  . В последнем равенстве справа стоит интегральная сумма для двойного интеграла
. В последнем равенстве справа стоит интегральная сумма для двойного интеграла  . Будем мельчить разбиение области так, чтобы
. Будем мельчить разбиение области так, чтобы  . Вследствие непрерывности функции
. Вследствие непрерывности функции  по теореме существования интегральная сумма при этом стремится к двойному интегралу
по теореме существования интегральная сумма при этом стремится к двойному интегралу  , т.е. в пределе получим
, т.е. в пределе получим  , что и требовалось доказать.
, что и требовалось доказать.
Если область  правильная в направлении оси Oх, то аналогично доказывается формула
правильная в направлении оси Oх, то аналогично доказывается формула  . Если
. Если  правильна в направлении обеих осей, то для вычисления двойного интеграла можно применять любую из эти формул:
правильна в направлении обеих осей, то для вычисления двойного интеграла можно применять любую из эти формул:  .
.
Если область не является правильной, её разбивают на правильные подобласти.
Дата добавления: 2015-07-20; просмотров: 137 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Теоремы об оценке интеграла. | | | Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах. |