Задачи на двойной интеграл.

16.1.6.1. Переход от двойного интеграла к повторному. Изменение порядка интегрирования. Переход к полярным координатам. Смысл этих задач - научиться быстро определять параметры (в декартовых координатах) и 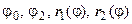(в полярных координатах), необходимые для перехода от двойного интеграла к повторному. Примеры:

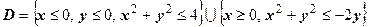1. Пусть область . Представить двойной интеграл по области в виде повторных. Перейти к полярным координатам.

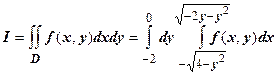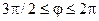Решение: область изображена на рисунке справа. Для левой части ; для правой - (уравнение правой полуокружности после выделения полных квадратов принимает вид ), поэтому . можно также описать неравенствами , поэтому . В полярных координатах уравнение левой четверти окружности имеет вид для (можно взять и отрезок ), правой полуокружности для (можно взять и отрезок ), поэтому .

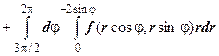2. 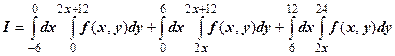. Изменить порядок интегрирования, перейти к полярным координатам.

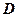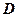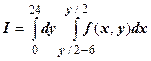Решение. Область - объединение трёх подобластей: . На рисунке изображена область и приведены уравнения прямых и обратных функций для линий, ограничивающих её. можно представить в виде , поэтому . В полярных координатах 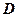представляется как объединение двух треугольников OCB и OBA. Уравнение прямой ОС: (можно получить и формально, перейдя к полярным координатам в её уравнении: ), прямой ОВ: , прямой СВ: , прямой ОА: , прямой АВ: . В результате .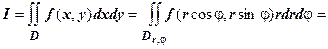

16.1.6.2. Вычисление двойного интеграла. Двойной интеграл вычисляется переходом к повторному. Рассмотрим ряд примеров.

1. .

Здесь область 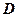(которую обязательно надо изобразить на чертеже) правильна в направлении обеих осей, поэтому вычисления по обеим формулам перехода имеют одинаковую трудоёмкость:

;

.

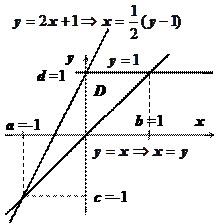
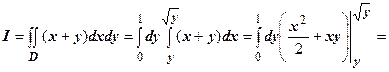
2. .

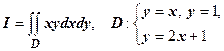Здесь область 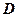тоже правильна в направлении обеих осей, однако верхняя граница состоит из двух кусков: , поэтому первый из повторных интегралов будет содержать два слагаемых:

;

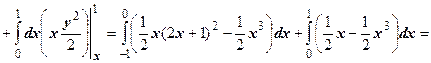
Этот пример проще решается по второй формуле.

3. .

Здесь переход к повторному интегралу по формуле бессмысленен, так как внутренний интеграл не берётся, в то же время второй повторный интеграл вычисляется без проблем:

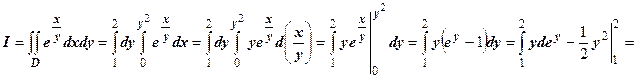
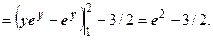
4.

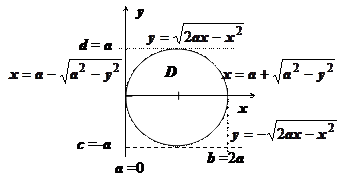
Здесь область D ограничена окружностью радиуса а, сдвинутой на а единиц по оси Ох. Уравнения для правой, левой, верхней и нижней полуокружностей приведены на рисунке. Повторные интегралы в декартовых координатах

, можно вычислить, но это достаточно трудоёмко. Попробуем перейти к полярным координатам (это имеет смысл, так как и подынтегральная функция, и кривая, ограничивающая D зависят от выражения 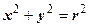). Переход к полярным координатам в уравнении окружности даёт , или . Это и есть уравнение границы в полярных координатах. Итак,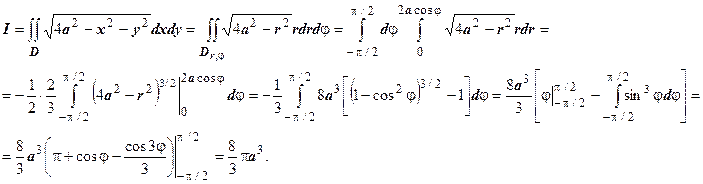

Ответ явно неправильный. Мы должны получить объём тела, расположенного в полупространстве , ограниченного цилиндром 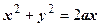и сферой 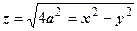радиуса 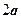сверху; в то время как получили половину объём верхнего полушара (рисунок справа). С такой ситуацией мы уже встречались, когда рассматривали приложения определённого интеграла. Ошибка делается, когда выражение заменяется на , а не на . Дальше необходимо отдельно рассматривать интервалы и . Избежать это можно, если воспользоваться симметрией и области, и подынтегральной функции относительно оси Ох, т.е. вычислять удвоенный интеграл по половине круга :

Дата добавления: 2015-07-20